보드선도(Bode Plot)은 제어 시스템의 설계 및 분석 목적으로 사용되는 그래픽 방법입니다. Bode Plot에서는 시스템의 주파수 응답을 그래픽으로 표현하는 방법을 단순화하는 데 도움이 되는 로그 스케일이 사용됩니다.
보드선도에서 크기의 로그와 위상 각도의 로그는 주파수의 로그 값에 대해 별도로 표시됩니다.

1. 보드선도의 필요성
주파수 응답 곡선의 기본 형태가 크기와 위상 각도 사이의 플롯을 나타내며 입력 주파수의 다양한 값, 즉 ω에 대해 표시됩니다. 이러한 플롯에서는 0에서 ∞까지의 ω 변동이 있으며 이에 대해 다양한 크기 및 위상각 값이 달성됩니다. 그러나 선형 스케일에서 크기와 위상각의 모든 값을 수용하는 것은 매우 어렵습니다.
따라서 H.W. Bode는 제어 시스템의 안정성 분석을 위해 다르지만 강력하고 유용한 방법을 제안했습니다.
2. 보드선도란?
극좌표 플롯에서는 다양한 ω 값에 대한 위상 각도 응답에 대한 크기 대 위상 각도 응답을 스케치하는 데 정규 선형 스케일이 사용됩니다. 그러나 bode plot에서는 일반 선형 눈금 대신 로그 눈금이 사용됩니다.
기본적으로 보드선도을 사용하여 시스템의 사인파 전달 함수는 두 개의 개별 플롯으로 나타낼 수 있습니다. 두 플롯 중 한 플롯은 크기 대 주파수에 해당하고 다른 플롯은 시스템의 위상각 대 주파수 응답에 해당합니다.
또한 두 플롯의 3개 매개변수는 모두 로그 스케일에 대해 스케치됩니다.
더 간단하게 Bode Plot은 2개의 플롯으로 구성되어 있다고 말할 수 있습니다.

1. 크기 플롯: 이 플롯에서 크기는 주파수의 로그 값에 대한 로그 값으로 표시됩니다.
전달 함수 G(jω)H(jω)의 경우 로그 값으로 크기를 표현하려면 다음을 찾아야 합니다.

그리고 이 크기 dB는 log10 ω에 대해 표시되며 아래 그림과 같이 표시됩니다.
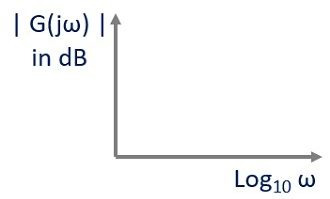
2. 위상 각도 플롯: 여기서 도 단위의 위상 각도는 주파수의 로그 값에 대해 스케치됩니다.
여기서 G(jω)의 각도 값(도)은 log10 ω에 대표 표시됩니다. 위상각 플롯의 일반적인 표현은 다음과 같습니다.

Bode Plot은 로그 스케일에 스케치되기 때문에 로그 플롯이라고도 하며 주파수에 대한 크기와 위상각의 광범위한 변화를 개별적으로 나타냅니다. 따라서 보드선도은 반 로그 그래프 용지에 스케치됩니다.
또한 두 플롯 모두에서 주파수의 로그 값이 x축을 기준으로 스케일링되는 것을 볼 수 있으므로 x축을 공통으로 유지할 수 있고 크기와 위상각 플롯을 모두 동일한 로그 페이퍼에 그릴 수 있습니다.
여기서 주목해야 할 점은 시스템 G(jω)H(jω)의 개방 루프 전달 함수가 있고 개방 루프 시스템의 주파수 응답을 사용하여 폐쇄 루프 안정성을 결정해야 한다고 가정합니다. 그런 다음 단순히 G (jω)가 아니라 G (jω) H (jω)의 크기와 위상 각도를 log10 ω에 대해 표시합니다.
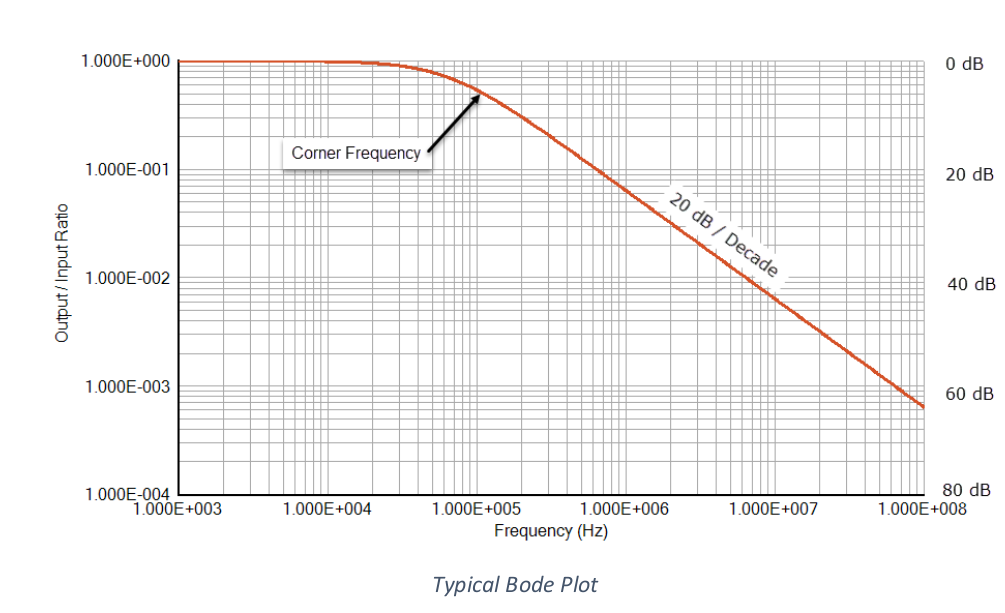
3. Open-Loop Transfer Function의 표준 인자에 대한 보드선도
개루프 전달 함수 G(jω)H(jω)의 경우 각 관련 요인에 대해 보드선도을 스케치하는 절차는 다음과 같습니다.
- s를 jω으로 바꿔 주어진 s-domain 전달 함수를 주파수 영역으로 변경합니다.
- 크기를 결정하고 주어진 공식에 따라 dB로 표현하십시오.

- 다음을 사용하여 위상 각도 φ(도)을 결정합니다.

- 또한 필요한 근사치를 고려하고 0에서 ∞ 사이의 다양한 ω 값에 대해 log ω에 대한 크기 및 위상각 그래프를 플로팅합니다.
이제 각 요소에 대해 자세히 알아보겠습니다.
1. 시스템 이득 K
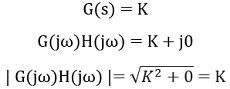
따라서 dB 단위의 크기는 다음과 같이 표현됩니다.
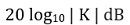
위에 주어진 크기 방정식에서 상수 K의 존재로 인해 크기는 0에서 ∞ 사이의 ω의 각 값에 대해 항상 일정합니다. 따라서 크기 플롯에서 이것은 x축에 평행한 직선으로 표시됩니다.
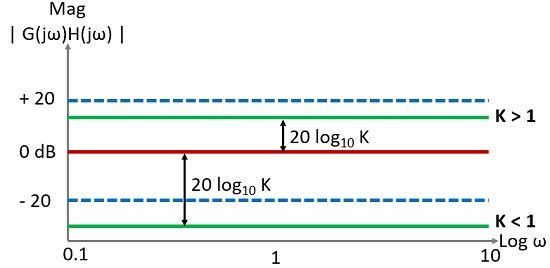
그러나 K>1의 경우 직선은 0dB 기준선보다 20log K 거리에 있습니다. K<1의 경우 선은 20 log K 거리에서 기준선 아래에 있습니다.
이것은 규모의 경우를 의미합니다. K의 효과는 변동을 나타내지 않습니다. 따라서 20log K dB는 모든 주파수에 대해 일정합니다.
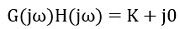
위상 각도 φ는 다음과 같습니다.
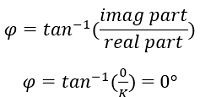
따라서 이것은 이득 계수 K가 위상 각도 플롯에 0°를 기여한다는 것을 보여줍니다.

따라서 K의 모든 양수 값에 대해 위상 플롯 사양은 변하지 않습니다. 그러나 K의 각 음수 값에 대해 0에서 ∞ 사이의 모든 K 값에 대한 플롯의 위상 각도에 -180°를 기여합니다.
2. 원점의 극점 또는 영점
원점에서 단일 극점을 고려하십시오.
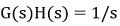
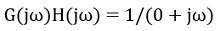
이제 크기를 계산하면 다음과 같습니다.
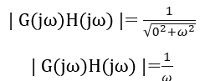
dB 단위의 크기는 다음과 같이 표시됩니다.
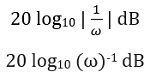
다음과 같이 정리할 수 있습니다.
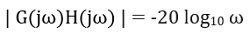
이제 ω의 다양한 값에 대한 크기 변화를 확인해 보겠습니다.
ω = 1인 경우,
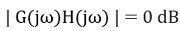
ω = 10인 경우,
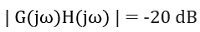
ω = 100인 경우,
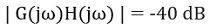
ω = 0.1인 경우,
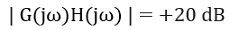
여기서는 빈도를 10의 배수로 취했으며, 이는 변화를 10decade로 나타냅니다.
또한 ω = 1의 경우 크기는 0dB이므로 -20dB의 기울기는 기준선, 즉 ω = 1에서 0dB와 교차합니다.
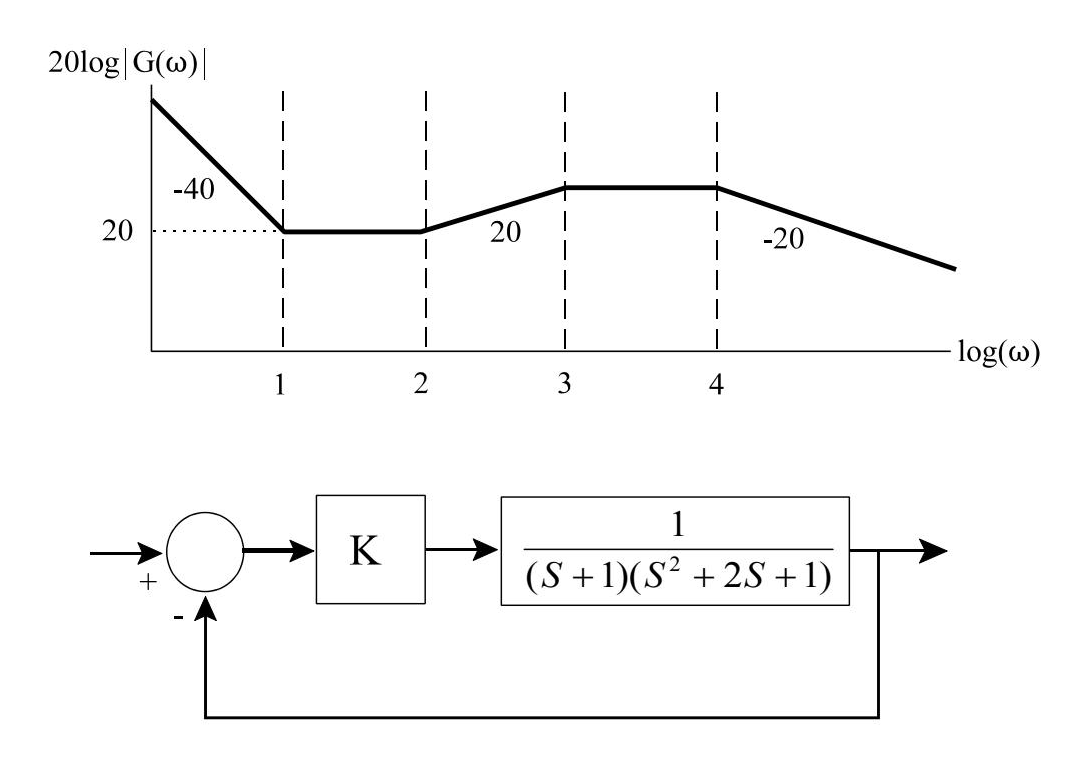
또한, 크기는 ω = 0.1 및 ω = 10에서 각각 + 20dB 및 -20dB입니다.
이 데이터를 기반으로 원점에서 1 극에 의한 크기 플롯은 다음과 같습니다.
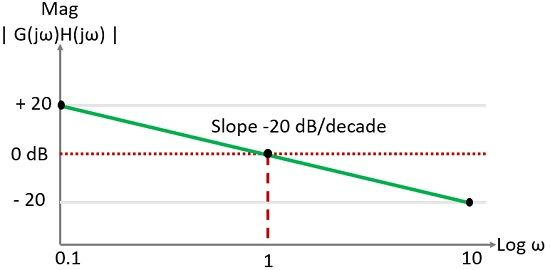
이제, 위상각을 계산하면,
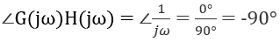
여기서 위상각은 ω와 무관합니다. 따라서 원점에서 1개의 극점에 대한 위상 플롯은 단순히 x축에 평행한 선입니다.
'데이터계측분석 > 데이터분석 기술자료' 카테고리의 다른 글
| 예측정비를 위한 상태 모니터링 방법 (0) | 2024.10.28 |
|---|---|
| 데이터베이스 서버의 종류와 차이점 (0) | 2024.07.27 |
| 신호처리의 평균편차, 표준편차와 분산 (0) | 2024.07.23 |
| 진동해석을 위한 파워 스펙트럼 밀도 계산방법 (0) | 2024.07.15 |
| 액티브 노이즈 캔슬링이란? (0) | 2023.10.20 |