진동 신호란?
진동은 평형점에 대해 진동이 발생하는 기계적 이벤트이며, 이러한 진동의 정보를 전달하는 시계열은 진동 신호라고 합니다. 평형점에서의 이러한 진동은 높은 샘플링 속도로 획득되어야 합니다.
진동 신호는 일반적으로 아래 그림과 같이 사인파로 표시될 수 있으며, 이는 분석하는 동안 기억해야 하는 몇 가지 중요한 속성을 가지고 있습니다.

- 진폭 또는 피크: 충격 이벤트 세부 정보를 제공하지만 이벤트의 지속 시간과 에너지를 고려하지 않습니다.
- 피크 투 피크: 파도의 최대 편위를 제공하며, 이는 변위 정보를 볼 때 유용합니다.
- RMS(제곱 평균 제곱근): 진동 신호의 에너지 함량과 직접적인 관련이 있기 때문에 가장 유용하며, 파형의 시간 이력을 고려하기 때문에 진동의 파괴 능력과 관련이 있습니다.
진동 신호는 비선형적이고 비정상적이며(대부분) 비정상 신호를 분석하는 것은 어려운 작업입니다.
Stationary신호와 Non-stationary 신호
정지 신호는 일정한 시간 주기를 갖는 사인파로 표시될 수 있는 반면, 정지 신호는 다양한 시간 주기를 갖는 사인파로 하는 사인파로 표시됩니다. 즉, 비고정 신호의 주파수가 시간에 따라 변하기 때문에 주파수 또는 스펙트럼 내용이 시간에 따라 변하지 않는 경우 신호를 고정이라고 할 수 있습니다.
정지 및 비정지 신호의 한 예는 주파수 분포와 함께 아래 그림에 나와 있습니다.

전력 스펙트럼이 있는 고정 및 비정상 신호의 예
진동 신호를 분석 기술
Empirical Mode Decomposition (EMD)
EMD는 비선형 및 비정상 신호를 여러 고유 모드 함수(IMF)와 잔기로 분해하는 적응형 방법입니다. EMD 알고리즘은 잔차가 상수, 단조 기울기 또는 극단값이 하나만 있는 함수로 유지될 때 종료되는 선별 과정을 기반으로 합니다.

힐버트 변환(Hilbert-Huang transform)과 EMD를 사용한 특정 주파수 대역 분리
경험적 모드 분해(EMD)는 진동 신호 S[n]를 협대역 IMF로 분해할 수 있습니다. 각 IMF는 다음 두 가지 필수 조건을 충족합니다.
- 데이터에서 극한의 계수와 제로 교차의 계수는 동일하거나 최대 1만큼 달라야 합니다
- 정의에 따르면 로컬 최대값과 로컬 최소값에서 얻은 봉투의 평균 값은 순간적으로 0입니다.
진동 신호를 좁은 대역으로 분해한 후 IMF에 Hilbert 변환(HT)을 적용하여 순간 주파수를 추출합니다. 예를 들어, 진동 신호의 5개 주파수 범위 기반 대역은 다음 그림에 나타나 있습니다. 이는 순간 주파수의 도움으로 EMD에 의해 분해된 진동 신호와 분리되어 있으며, 이는 모든 샘플에 대해 단일 주파수 값을 결정하는 HT를 사용하여 모든 IMF에서 추출됩니다.

(I) 델타: 0–4 Hz, (II) 세타: 4–8 Hz, (III) 알파: 8–13 Hz, (IV) 베타: 13–30 Hz, (V) 감마: 30–60 Hz
상기 방법을 사용하여 진동 신호의 다중 리듬을 추출할 수 있으며, 이는 다양한 측면에서 유용합니다.
진동 신호에 대한 시간-주파수 분석을 수행하는 몇 가지 일반적인 방법은 다음과 같습니다:
- 단시간 푸리에 변환(STFT)
- 웨이블릿 변환(연속/이산 WT)
- 스톡웰 트랜스폼(ST)
- Wigner-Ville 분포 (WVD)
- SPWVD(Smooth Pseudo Wigner-Ville 분포)
아래 그림에 나와 있는 진동 신호(낮고 높은 주파수 포함)의 매우 간단한 예를 사용하여 시간 주파수 표현을 이해하려고 합니다.

두 개의 다른 주파수를 가진 진동 신호
이제 다양한 방법을 사용하여 주어진 신호의 시간-주파수 표현(TFR)을 살펴보겠습니다.
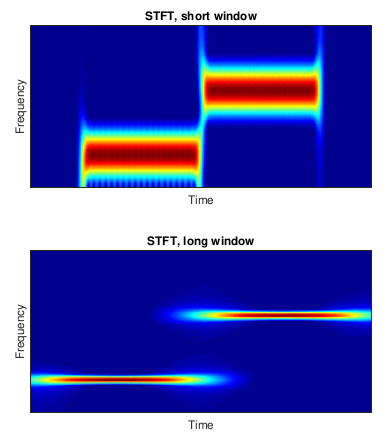
짧고 긴 윈도우를 갖는 주어진 신호의 단시간 푸리에 변환
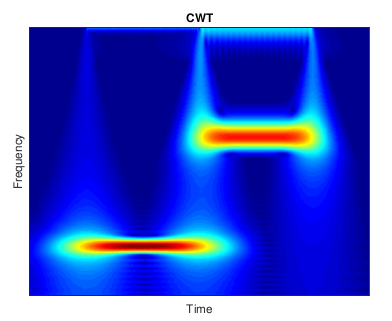
주어진 신호의 연속 웨이블릿 변환
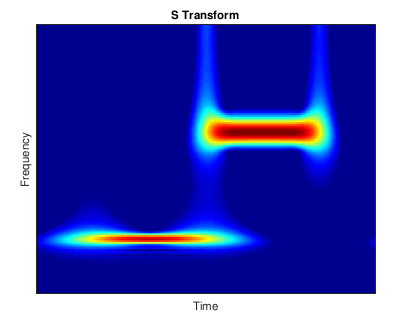
주어진 신호의 ST
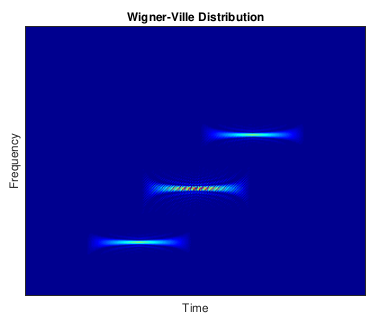
WVD를 사용하는 주어진 신호의 TFR,
여기서 교차항 아티팩트가 높은 진폭으로 발생한다는 것을 알 수 있습니다
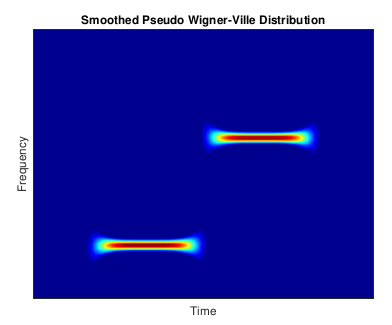
여기서 변환의 목적은 차별적인 시간 및 주파수 특징을 시각적으로 표시하는 것이므로 크기만 표시됩니다. 이 블로그를 통해 다양한 방법으로 계산된 스펙트럼이 어떻게 진동 신호를 차별적으로 나타내는지 이해할 수 있습니다. 매개 변수의 선택은 신호 속성 및/또는 결과의 추가 사용 또는 후속 처리에 따라 달라집니다. 중요한 측면은 원하는 시간 및 빈도의 해상도와 아티팩트의 허용 가능성입니다. 예를 들어, 교차 기간 아티팩트를 탐지하려면 아티팩트 SPWVD가 더 나은 옵션임을 무시하고 WVD를 고려해야 합니다.
방법을 선택하는 또 다른 예는 위의 그림(짧고 긴 창이 있는 STFT)이 짧은 창과 긴 창에 의한 스펙트럼 프로그램을 포함하는 것일 수 있으며, 여기서 주파수의 고해상도와 저해상도를 각각 볼 수 있습니다. 응용 프로그램에 따라 창 크기를 선택할 수 있습니다. 그러나 고해상도 주파수가 증가하면 시간 분해능이 감소합니다. 동시에 두 가지 모두에서 높은 해상도를 가질 수는 없지만 창 크기를 사용하면 시간과 주파수 해상도를 균형 있게 조정할 수 있으며 요구 사항에 따라 창 크기를 최적화할 수 있습니다.
이 블로그에 포함된 방법과 관련하여 다음과 같은 몇 가지 사항이 있으며, 요구 사항에 따라 적절한 방법을 선택하는 데 도움이 될 수 있습니다.
- STFT - 해석이 용이함; 빠른 푸리에 변환을 이용한 빠른 구현; 그러나 제한적이고 고정된 해상도
- WT — 분해능이 고정되지 않음, 분해능은 주파수(다중 스케일 특성)에 따라 다릅니다; 일반적으로 주파수가 낮은 구성요소는 주파수 분해능이 더 만족스럽고 시간 분해능이 더 거칠며 주파수가 높은 경우에는 역방향입니다
- ST — 빈도가 높은 내용을 강조하는 경향이 있습니다.
- WVD - 제한된 해상도 극복(각 시간 단계의 주파수 내용 계산), 빠른 구현이 아닌 강력한 아티팩트
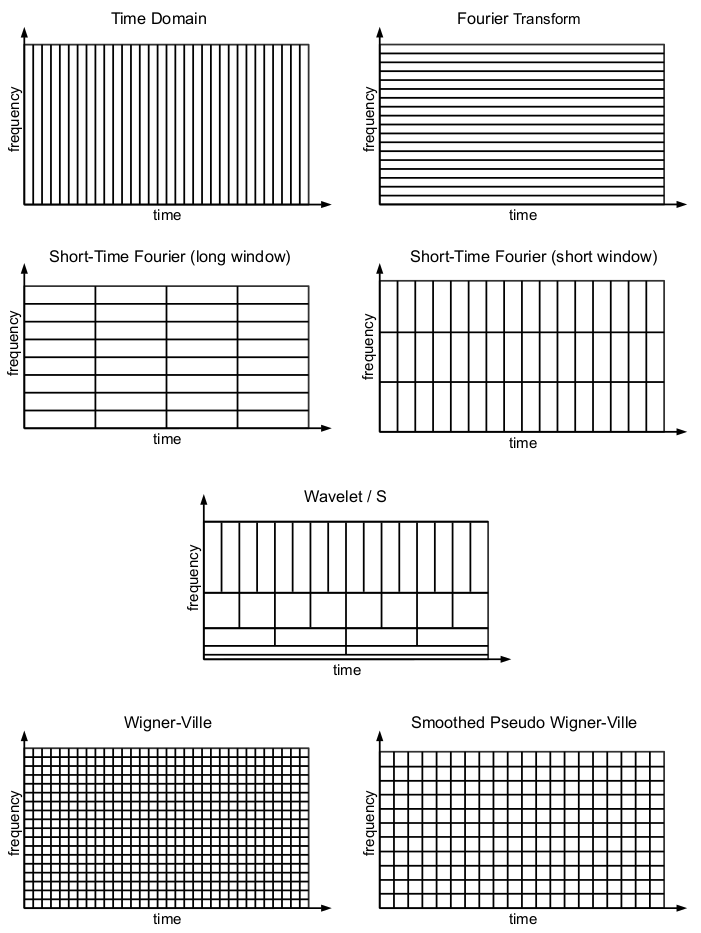
시간 영역 표현과 비교를 위한 표준 푸리에 스펙트럼을 포함한 변환 해상도의 도식이 아래에 나와 있습니다.
'데이터계측분석 > 데이터계측 기술자료' 카테고리의 다른 글
| 속도와 거리로 가속도 계산하기 (0) | 2023.05.23 |
|---|---|
| 데이터계측의 기초 (0) | 2023.05.20 |
| 데이터 수집 시스템(Data Acquisition System) (0) | 2023.05.12 |
| 제어계측 시스템에 적합한 하드웨어 인터페이스 선정방법 (0) | 2023.05.03 |
| 옴의 법칙과 기본 아날로그 회로 개념 (0) | 2023.05.03 |