수학의 적분은 면적, 부피, 변위 등과 같은 많은 유용한 양을 찾는 데 사용됩니다. 적분에 대해 말할 때 일반적으로 정적분과 관련이 있습니다. 무한 적분은 역도함수에 사용됩니다. 적분은 미분(변수에 대한 함수의 변화율을 측정)을 제외하고 수학의 두 가지 주요 미적분 주제 중 하나입니다.
적분 정의
적분은 불연속 데이터의 합계를 나타냅니다. 적분은 단독으로 측정할 수 없는 작은 데이터 모음으로 인해 발생하는 면적, 변위, 부피를 설명하는 함수를 찾기 위해 계산됩니다. 넓은 의미에서 미적분학에서 한계의 개념은 대수학과 기하학이 구현되는 곳에서 사용됩니다. 한계는 거리가 거의 0이 될 때까지 서로 가까워지는 방법과 같이 그래프의 점 결과를 연구하는 데 도움이 됩니다. 우리는 미적분학에는 두 가지 주요 유형이 있다는 것을 알고 있습니다.
- 미분 Differential Calculus
- 적분 Integral Calculus
적분의 개념은 다음과 같은 유형의 문제를 해결하기 위해 개발되었습니다.
- 도함수가 주어졌을 때 문제 함수를 찾기 위해
- 특정 제약 조건에서 함수 그래프로 경계가 지정된 영역을 찾기 위해
이 두 가지 문제는 정적분과 무한 적분으로 구성된 "적분 미적분학"이라는 개념의 개발로 이어집니다. 미적분학에서 함수를 미분하고 함수를 적분하는 개념은 미적분학의 기본 정리라는 정리를 사용하여 연결됩니다.
적분
수학에서 적분은 전체를 찾기 위해 부분을 더하거나 합산하는 방법입니다. 기능을 부분으로 줄이는 차별화의 역 과정입니다. 이 방법은 방대한 규모에서 합계를 찾는 데 사용됩니다. 작은 덧셈 문제의 계산은 수동으로 또는 계산기를 사용하여 수행할 수 있는 쉬운 작업입니다. 그러나 한계가 무한대에 도달 할 수있는 큰 덧셈 문제의 경우 적분 방법이 사용됩니다. 적분과 미분은 모두 미적분학의 중요한 부분입니다.
수학자 베른하르트 리만(Bernhard Riemann)
"적분은 곡선 영역을 얇은 수직 슬래브로 분할하여 면적을 근사화하는 제한 절차를 기반으로 합니다."
이제 이것이 무엇을 의미하는지 이해해 보겠습니다:
미분 미적분이 무엇인지 확인하기 위해 그래프에서 선의 기울기의 예를 들어 보겠습니다:
일반적으로 기울기 공식을 사용하여 기울기를 찾을 수 있습니다. 그러나 곡선의 영역을 찾으라고 주어진다면 어떨까요? 곡선의 경우 점의 기울기가 다양하며 곡선의 기울기를 찾기 위해 미분 미적분학이 필요합니다.
적분 – 미분의 역 과정
미분이 함수의 도함수를 찾는 과정이고 적분은 함수의 도함수를 찾는 과정이라는 것을 알고 있습니다. 그래서, 이 과정들은 서로 반대입니다. 그래서 우리는 적분이 미분의 역과정이라고 말할 수 있고, 그 반대라고 말할 수 있습니다. 통합은 반미분화라고도 합니다. 이 과정에서 우리는 함수의 도함수를 제공받고 함수(즉, 원시)를 알아내도록 요청받습니다.
sinx의 미분이 cosx라는 것을 알고 있습니다.
그것은 수학적으로 다음과 같이 쓰여집니다:
(d/sinx) sinx = cos x …(1)
여기서, cosx는 sinx의 도함수입니다. sinx는 함수 cosx의 도함수입니다. 또한 실수 "C"는 상수 함수로 간주되며 상수 함수의 도함수는 0입니다.
따라서 방정식 (1)은 다음과 같이 쓸 수 있습니다
(d/dx) (sinx + C)= cos x +0
(d/dx) (sinx + C)= cos x
여기서 "C"는 임의의 적분 상수 또는 상수입니다.
일반적으로 다음과 같이 함수를 작성할 수 있습니다:
(d/dx) [F(x)+C] = f(x), 여기서 x는 구간 I에 속합니다.
"f"의 반파생을 나타내기 위해 적분 기호 "∫" 기호가 도입되었습니다. 함수의 반파생은 ∫f(x) dx로 표시됩니다. 이것은 x에 대한 함수 "f"의 무한 적분으로도 읽을 수 있습니다.
따라서 함수(적분)의 반파생의 기호적 표현은 다음과 같습니다:
y = ∫ f(x) dx
∫ f(x) dx = F(x) + C.
수학의 적분
수학에서 두 가지 유형의 적분을 접하게 될 것입니다.
- 확정적분
- 부정적분
확정 적분
상한과 하한을 포함하는 적분은 명확한 적분입니다. 실제 라인에서 x는 거짓말로 제한됩니다. 리만 적분(Riemann Integral)은 확정적분의 다른 이름입니다.
명확한 적분은 다음과 같이 표현됩니다.
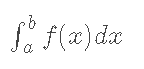
부정적분
무한 적분은 상한과 하한 없이 정의됩니다. 다음과 같이 표시됩니다.

여기서 C는 상수이고 함수 f(x)를 적분이라고 합니다.
통합 수식
아래에서 고급 수학 계산에 일반적으로 사용되는 적분 또는 적분 공식을 확인하십시오. 이러한 공식을 사용하면 통합과 관련된 모든 문제를 쉽게 해결할 수 있습니다.
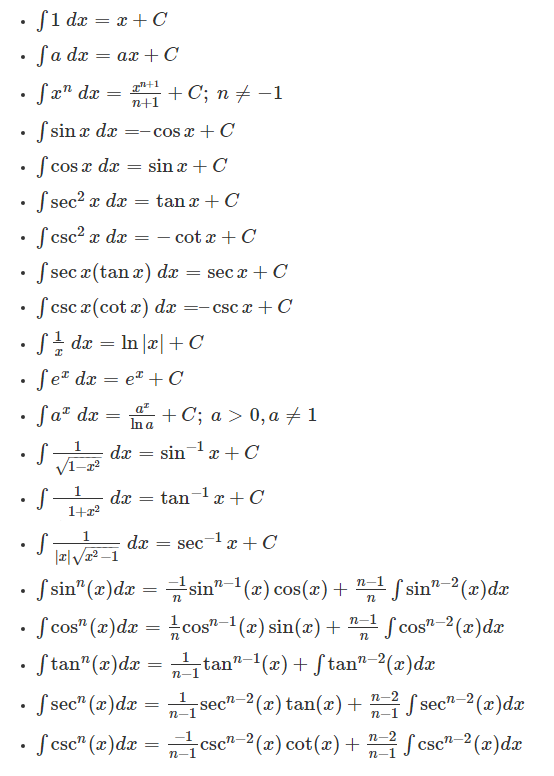
'데이터계측분석 > 전기전자 기술자료' 카테고리의 다른 글
| DPDT(Double Pole, Double Throw) 스위치 (0) | 2023.05.26 |
|---|---|
| 무접점 계전기(SSR), 전기기계계전기(EMR)의 차이점 (0) | 2023.05.26 |
| 단상과 3상 전원의 차이점 (0) | 2023.05.25 |
| 3상 교류 전류 (Three-Phase Power) (0) | 2023.05.25 |
| MCB, MCCB, ELCB 및 RCD의 차이점 (회로 차단기) (0) | 2023.05.24 |