다이나믹 신호 분석기의 일반적인 응용 분야는 기계 시스템의 주파수 응답 기능(FRF)을 측정하는 것입니다. 이를 네트워크 분석이라고도 하며, 시스템 입력과 출력이 동시에 측정됩니다.
이러한 다중 채널 측정을 통해 분석기는 시스템이 입력을 "변경"하는 방법을 측정할 수 있습니다. 시스템이 선형인 경우(일반적인 가정) 이 "변경"은 주파수 응답 함수(FRF)에 의해 완전히 설명됩니다.
사실, 선형적이고 안정적인 시스템의 경우 모든 입력에 대한 시스템의 응답은 주파수 응답 함수를 아는 것만으로도 예측할 수 있습니다.
광대역 랜덤, 사인, 스텝 또는 과도 신호는 테스트 및 측정 어플리케이션에서 여기 신호로 널리 사용됩니다.
그림 1은 여기 신호 x가, UUT(Unit Under Test)에 적용되고, y로 표시된 하나 또는 다수의 응답을 생성할 수 있음을 예시한다. 입력과 출력 사이의 관계는 전달 함수 또는 주파수 응답 함수로 알려져 있으며 H(y,x)로 표시됩니다.
일반적으로 전달 함수는 시스템이 입력 신호 크기와 위상을 여기 주파수의 함수로 수정하는 방법을 설명하는 복잡한 함수입니다.
주파수 응답 기능(FRF)은 다음과 같이 설명됩니다.
- - 주파수의 함수로서의 이득
- - 주파수의 함수로서의 위상
- - 공진 주파수
- - 댐핑 팩터
- - 총 고조파 왜곡
- - 비선형성
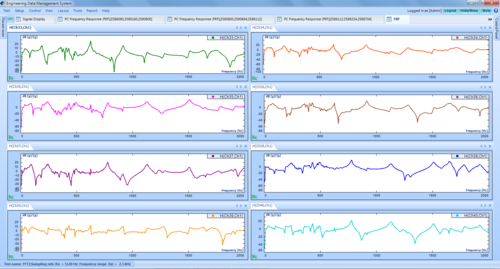

그림 1: 왼쪽 - 하나의 응답이 있는 UUT; 오른쪽 - 두 개의 응답이 있는 UUT
주파수 응답은 FFT, 광대역 무작위 들뜸이 있는 교차 전력 스펙트럼 방법을 사용하여 측정됩니다. 광대역 여기는 가우스 분포를 갖는 실제 랜덤 노이즈 신호이거나 사용자가 진폭 분포를 정의할 수 있는 유사 랜덤 신호일 수 있습니다.
잘 구현된 무작위 여기 신호는 주파수 대역 제한을 받아야 하고 분석 주파수 범위의 상한에 의해 제어되어야 하므로 광대역이라는 용어는 오해의 소지가 있습니다. 즉, 여기는 계측기로 측정할 수 있는 주파수 이상의 주파수를 자극해서는 안 됩니다. 랜덤 생성기는 분석 주파수 범위까지의 랜덤 신호만 생성합니다. 이는 또한 여기 에너지를 유용한 주파수 범위에 집중시킵니다.
광대역 무작위 들뜸을 사용하는 장점은 짧은 시간에 전체 주파수 범위를 들뜸할 수 있어 총 테스트 시간이 짧다는 것입니다. 광대역 여기의 단점은 주파수 콘텐츠가 짧은 기간 내에 광범위하게 확산된다는 것입니다. 각 주파수 포인트에서 여자의 에너지 기여는 총 신호 에너지보다 훨씬 적습니다(대략 -30 ~ -50dB). 주파수 응답 함수(FRF) 추정을 위한 평균 수치가 크더라도 광대역 신호는 UUT의 극단적인 동적 특성을 효과적으로 측정하지 못할 것입니다.
반면 스위프 사인 측정은 각 주파수 포인트에서 측정을 최적화합니다. 여기는 사인파이기 때문에 모든 에너지가 단일 주파수에 집중되어 광대역 여기에서 동적 범위 페널티를 제거합니다. 또한 주파수 응답 크기가 감소하면 응답의 추적 필터가 매우 작은 사인 신호를 수집하는 데 도움이 될 수 있습니다. 각 주파수에서 입력 범위를 최적화하기만 하면 측정의 동적 범위를 150dB 이상으로 확장할 수 있습니다.
스윕 사인을 사용하여 주파수 응답 기능 측정
고정 주파수의 사인 신호는 다음 주파수 응답 함수 공식으로 표시됩니다:

여기서 t는 시간을 나타냅니다. 스위핑 사인 신호는 일반적으로 두 개의 한계로 제한되는 변화하는 주파수를 가지고 있습니다. 주파수 변경은 다양한 사용자 요구 사항에 따라 선형 스케일 또는 로그 스케일로 이루어질 수 있습니다.
스윕 사인 신호는 다음 파라미터로 정의할 수 있습니다.
- 저주파 경계(단순히 저주파 또는 flow라고 함)
- 고주파 또는 fHigh라고 하는 고주파 경계
- 스위핑 모드(로그 또는 선형)
- 스위프 모드가 로그인 경우 스위프 속도(옥타브/분), 스위프 모드가 선형인 경우 Hz/초)
- 시간 및 주파수의 상수 또는 변수가 될 수 있는 사인 신호 A(f, t)의 진폭입니다.

순간 주파수 f는 스위핑 사인의 현재 주파수를 나타냅니다. 변화하는 변수이며 일반적으로 화면에 스순간 주파수 f는 스위핑 사인의 현재 주파수를 나타냅니다. 이것은 변화하는 변수이며 일반적으로 화면에 스위핑 주파수로 표시됩니다.
Weeping(소거) 주파수는 Hold(보류), Resume(재개), Jump(점프) 또는 Pause(일시 중지) 컨트롤을 사용하여 테스트 중에 수동으로 제어할 수도 있습니다.
일부 DSA(Digital Signal Analysis) 제품이 시퀀스에 여러 개의 개별 스텝 사인 톤이 있는 스위프 사인 테스트를 사용하는 것과 달리, CI 스위프 사인 테스트는 진정한 디지털 합성 기술을 사용하여 한 주파수에서 다른 주파수로 극도의 아날로그와 유사한 부드러운 전환으로 사인 스위프를 생성합니다. 이렇게 하면 테스트 중에 UUT에 충격을 줄 수 있는 급격한 전환이 발생하지 않습니다. 그림 2는 1.0 Vpk의 일반적인 스윕 사인 신호를 보여줍니다.
스위프된 사인은 선형 또는 로그 모드에서 스위프할 수 있습니다. 선형 스위프는 주파수가 Hz/초 단위로 일정한 속도로 변경됨을 의미합니다. 이 경우 스위프 속도는 일정하며 모든 주파수에서 동일합니다. 또는 스위핑 모드를 로그 또는 로그로 설정할 수 있습니다. 로그 모드에서는 스위프 속도가 저주파에서는 느리고 고주파에서는 빠릅니다. 로그 모드에서 스위핑 속도 단위는 옥타브/분입니다.
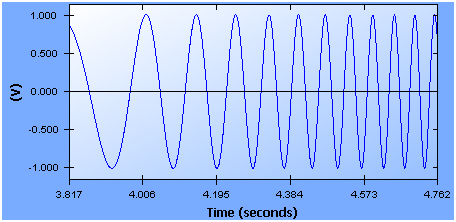
그림 2. 일반적인 디지털 합성 스윕 사인 신호.
수백 개의 FRF 신호 측정 및 표시 기능
PC FRF에서 FRF 신호는 스파이더 대신 PC에 의해 계산됩니다. PC FRF는 스파이더의 프로세서보다 훨씬 강력한 PC의 리소스에 의존하기 때문에 수백 개의 FRF 신호를 동시에 계산할 수 있습니다. 여러 채널을 기준 채널로 지정할 수 있습니다.
선형 시스템의 입력(힘 들뜸)과 출력(진동 응답) 사이의 관계는 다음과 같습니다:
{Y} = [H]{X}
여기서 {Y}와 {X}는 모델의 서로 다른 DOF에서 각각 반응 스펙트럼과 여기 스펙트럼을 포함하는 벡터이며, [H]는 이러한 DOF 사이의 FRF를 포함하는 행렬입니다.

여기서 Yi는 DOFi의 출력 스펙트럼, Xj는 DOFj의 입력 스펙트럼, Hij는 DOFj와 DOFi 사이의 FRF입니다. 출력은 각 입력에 의해 발생한 개별 출력의 합계입니다.
FRF는 측정된 입력과 출력 사이의 자동 및 교차 스펙트럼으로부터 추정됩니다. 주어진 측정 상황(노이즈 존재, 주파수 분해능 등)에서 추정을 최적화하기 위해 다양한 계산 방식(추정기)을 사용할 수 있습니다.
단일 입력의 고전적인 경우, 위의 방정식은 입력이 DOF j에 있는 임의의 DOFi에서의 출력을 다음과 같이 제공합니다:

입력이 j를 제외한 모든 DOF에서 0이기 때문입니다.

The FRF Hij 다음과 같은 다양한 고전적 추정기를 사용하여 추정할 수 있습니다.
H1 = Gxy/Gxx
또는
H2 = gyy/gyx
여기서 Gxx와 Gyy는 각각 입력과 출력의 자동 스펙트럼, Gxy는 입력과 출력 사이의 교차 스펙트럼, Gyx는 출력과 입력 사이의 교차 스펙트럼(즉, Gxy의 복잡한 공역)입니다.
H1은 평균을 통해 출력에서 상관 관계가 없는 노이즈의 영향을 제거할 수 있는 기능을 가지고 있는 반면, H2는 평균을 통해 입력에서 상관 관계가 없는 노이즈의 영향을 제거할 수 있습니다.
H1에 비해, H2는 불충분한 주파수 분해능(분해능 편향 오류라고 함)으로 인해 발생하는 공진 피크에서 바이어스 오류에 덜 취약합니다.
'데이터계측분석 > 데이터분석 기술자료' 카테고리의 다른 글
| 진동해석을 위한 파워 스펙트럼 밀도 계산방법 (0) | 2024.07.15 |
|---|---|
| 액티브 노이즈 캔슬링이란? (0) | 2023.10.20 |
| THD, Total Harmonic Distortion (왜곡) (0) | 2023.06.03 |
| 고속 푸리에 변환 FFT - Fast Fourier Transformation (0) | 2023.05.29 |
| 진동 분석 (Vibration Analysis) (0) | 2023.05.28 |