MATLAB은 기호 도함수를 계산하기 위한 diff 명령을 제공합니다. 가장 간단한 형태로, 미분하려는 함수를 인수로 전달합니다.
예를 들어, 함수의 도함수를 계산해 봅시다
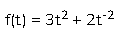
예시
스크립트 파일을 만들고 다음 코드를 입력합니다.
syms t
f = 3*t^2 + 2*t^(-2);
diff(f)
위의 코드가 컴파일되고 실행될 때, 다음과 같은 결과를 생성 합니다.
ans =
6*t - 4/t^3
다음은 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)
옥타브는 코드를 실행하고 다음과 같은 결과를 반환합니다
ans =
-(4.0)*t^(-3.0)+(6.0)*t
미분의 기본 규칙 검증
함수의 미분을 위한 다양한 방정식이나 규칙을 간략하게 설명하고 이러한 규칙을 확인봅시다. 이를 위해 1차 도함수에 대해 f'(x)를 쓰고 2차 도함수에 대해 f"(x)를 씁니다.
다음은 미본 규칙입니다 -
규칙 1
모든 함수 f와 g와 임의의 실수 a와 b는 함수의 도함수입니다.
x에 대한 h(x) = af(x) + bg(x)는 -로 주어진다.
h'(x) = af'(x) + bg'(x)
규칙 2
합과 뺄셈 규칙은 f와 g가 두 함수이고 f'와 g'가 각각 도함수인 경우
(f + g)' = f' + g'
(f - g)' = f' - g'
규칙 3
곱셈 규칙은 f와 g가 두 함수이고 f'와 g'가 각각 도함수인 경우
(f.g)' = f'.g + g'.f
규칙 4
몫 규칙은 f와 g가 두 함수이고 f'와 g'가 각각 도함수인 경우
(f/g)' = (f'.g - g'.f)/g2
규칙 5
다항식 또는 기본 거듭제곱 규칙은 다음과 같이 말합니다.

그러면

이 규칙의 직접적인 결과는 모든 상수의 도함수가 0, 즉 y = k이면 임의의 상수인 경우
f' = 0
규칙 6
Chain 규칙은 x에 대한 함수 h(x) = f(g(x))의 함수의 도함수는 다음과 같다고 명시합니다.
h'(x)= f'(g(x)).g'(x)
예시
스크립트 파일을 만들고 다음 코드를 입력합니다.
syms x
syms t
f = (x + 2)*(x^2 + 3)
der1 = diff(f)
f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)
f = (x^2 + 1)^17
der5 = diff(f)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)
파일을 실행할 때, MATLAB은 다음과 같은 결과를 표시합니다 -
f =
(x^2 + 3)*(x + 2)
der1 =
2*x*(x + 2) + x^2 + 3
f =
(t^(1/2) + t^3)*(t^2 + 3)
der2 =
(t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
f =
(x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 =
(2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
f =
(2*x^2 + 3*x)/(x^3 + 1)
der4 =
(4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
f =
(x^2 + 1)^17
der5 =
34*x*(x^2 + 1)^16
f =
1/(t^3 + 3*t^2 + 5*t - 9)^6
der6 =
-(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7
다음은 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)
옥타브는 코드를 실행하고 다음과 같은 결과를 반환합니다 -
f =
(2.0+x)*(3.0+x^(2.0))
der1 =
3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =
(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =
(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =
(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =
(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =
(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =
(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =
(1.0+x^(2.0))^(17.0)
der5 =
(34.0)*(1.0+x^(2.0))^(16.0)*x
f =
(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =
-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)
지수함수, 로그함수, 삼각함수의 도함수
다음 표는 일반적으로 사용되는 지수, 로그 및 삼각 함수의 도함수를 제공합니다

예시
스크립트 파일을 만들고 다음 코드를 입력합니다.
syms x
y = exp(x)
diff(y)
y = x^9
diff(y)
y = sin(x)
diff(y)
y = tan(x)
diff(y)
y = cos(x)
diff(y)
y = log(x)
diff(y)
y = log10(x)
diff(y)
y = sin(x)^2
diff(y)
y = cos(3*x^2 + 2*x + 1)
diff(y)
y = exp(x)/sin(x)
diff(y)
파일을 실행할 때, MATLAB은 다음과 같은 결과를 표시합니다 -
y =
exp(x)
ans =
exp(x)
y =
x^9
ans =
9*x^8
y =
sin(x)
ans =
cos(x)
y =
tan(x)
ans =
tan(x)^2 + 1
y =
cos(x)
ans =
-sin(x)
y =
log(x)
ans =
1/x
y =
log(x)/log(10)
ans =
1/(x*log(10))
y =
sin(x)^2
ans =
2*cos(x)*sin(x)
y =
cos(3*x^2 + 2*x + 1)
ans =
-sin(3*x^2 + 2*x + 1)*(6*x + 2)
y =
exp(x)/sin(x)
ans =
exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2
다음은 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)
옥타브는 코드를 실행하고 다음과 같은 결과를 반환합니다 -
y =
exp(x)
ans =
exp(x)
y =
x^(9.0)
ans =
(9.0)*x^(8.0)
y =
sin(x)
ans =
cos(x)
y =
tan(x)
ans =
1+tan(x)^2
y =
cos(x)
ans =
-sin(x)
y =
log(x)
ans =
x^(-1)
y =
sin(x)^(2.0)
ans =
(2.0)*sin(x)*cos(x)
y =
cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =
-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =
sin(x)^(-1)*exp(x)
ans =
sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)
Higher Order Derivatives
함수 f의 더 높은 도함수를 계산하기 위해 diff(f,n) 구문을 사용합니다.
2차 도함수를 계산해 보겠습니다.

f = x*exp(-3*x);
diff(f, 2)
MATLAB은 코드를 실행하고 다음과 같은 결과를 반환합니다 -
ans =
9*x*exp(-3*x) - 6*exp(-3*x)
다음은 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)
옥타브는 코드를 실행하고 다음과 같은 결과를 반환합니다 -
ans =
(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)
예시
이 예에서는 문제를 해결해 보겠습니다. 함수 y = f(x) = 3 sin(x) + 7 cos(5x)라고 가정합니다. 방정식 f" + f = -5cos(2x)가 참인지 확인해야 합니다.
스크립트 파일을 만들고 그것에 다음 코드를 입력합니다.
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
파일을 실행할 때, 그것은 다음과 같은 결과를 표시합니다.
No, the equation does not hold true
Value of LHS is:
-168*cos(5*x)
다음은 위의 계산에 해당하는 옥타브입니다.
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
옥타브는 코드를 실행하고 다음과 같은 결과를 반환합니다 -
No, the equation does not hold true
Value of LHS is:
-(168.0)*cos((5.0)*x)
곡선의 최대값과 최소값 찾기
그래프에 대한 국소 최대값과 최솟값을 검색하는 경우 기본적으로 특정 국소에서 함수 그래프의 최고점 또는 최저점 또는 기호 변수의 특정 값 범위를 찾고 있습니다.
함수 y = f(x)의 경우 그래프에서 그래프의 기울기가 0인 점을 정지 점이라고 합니다. 즉, 정지점은 f'(x) = <>입니다.
미분하는 함수의 정지점을 찾으려면 도함수를 0으로 설정하고 방정식을 풀어야 합니다.
예시
다음 함수의 stationary point를 구해 봅시다.

다음 단계를 수행하십시오 -
먼저 함수를 입력하고 그래프를 그려 보겠습니다.
syms x
y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function
ezplot(y)
MATLAB은 코드를 실행하고 다음과 같은 플롯을 반환합니다 -
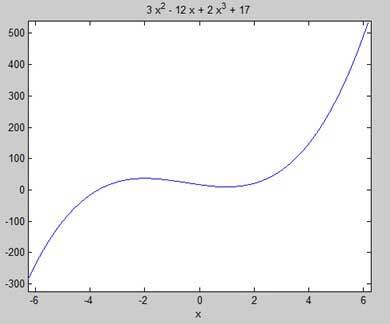
여기에 위의 예에 대한 옥타브에 해당하는 코드입니다 -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.eps
목표는 그래프에서 국소 최대값과 최소값을 찾는 것이므로 그래프에서 구간 [-2, 2]에 대한 국소 최대값과 최소값을 구해 보겠습니다.
syms x
y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function
ezplot(y, [-2, 2])
MATLAB은 코드를 실행하고 다음과 같은 플롯을 반환합니다 -
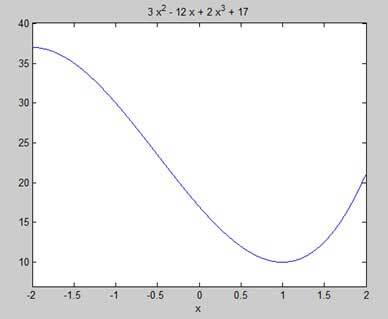
여기에 위의 예에 대한 옥타브에 해당하는 코드입니다 -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.eps
다음으로 도함수를 계산해 보겠습니다.
g = diff(y)
MATLAB은 코드를 실행하고 다음과 같은 결과를 반환합니다 -
g =
6*x^2 + 6*x - 12
여기에 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
옥타브는 코드를 실행하고 다음과 같은 결과를 반환합니다 -
g =
-12.0+(6.0)*x+(6.0)*x^(2.0)
도함수 g를 풀어 0이 되는 값을 구해 보겠습니다.
s = solve(g)
MATLAB은 코드를 실행하고 다음과 같은 결과를 반환합니다 -
s =
1
-2
다음은 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
옥타브는 코드를 실행하고 다음과 같은 결과를 반환합니다 -
g =
-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =
-2
1
따라서 임계점 x = 1, -2에서 함수 f를 평가해 보겠습니다. subs 명령을 사용하여 기호 함수의 값을 대체할 수 있습니다.
subs(y, 1), subs(y, -2)
MATLAB은 코드를 실행하고 다음과 같은 결과를 반환합니다 -
ans =
10
ans =
37
다음은 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)ans =
10.0
ans =
37.0-4.6734207789940138748E-18*I
따라서 [-2,2] 구간에서 함수 f(x)의 최소값과 최대값은 10과 37입니다.

미분 방정식 풀기
MATLAB은 기호적으로 미분 방정식을 풀기 위한 dsolve 명령을 제공합니다.
단일 방정식에 대한 해를 찾기 위한 dsolve 명령의 가장 기본적인 형태는 다음과 같습니다.
dsolve('eqn')
여기서 EQN은 방정식을 입력하는 데 사용되는 텍스트 문자열입니다.
MATLAB이 C1, C2 등의 레이블을 지정하는 임의 상수 집합이 포함된 기호 해를 반환합니다.
문제에 대한 초기 및 경계 조건을 다음과 같은 식에 따라 쉼표로 구분된 목록으로 지정할 수도 있습니다
dsolve('eqn','cond1', 'cond2',…)
dsolve 명령을 사용하기 위해 도함수는 D로 표시됩니다. 예를 들어, f'(t) = -2*f + cost(t)와 같은 방정식은 -로 입력됩니다.
'Df = -2*f + cos(t)'
더 높은 도함수는 도함수의 순서에 따라 D를 따라 표시됩니다.
예를 들어, 방정식 f"(x) + 2f'(x) = 5sin3x는 -로 입력해야 합니다.
'D2y + 2Dy = 5*sin(3*x)'
5차 미분 방정식의 간단한 예를 들어 보겠습니다: y' = 5y.
s = dsolve('Dy = 5*y')
MATLAB은 코드를 실행하고 다음과 같은 결과를 반환합니다 -
s =
C2*exp(5*t)
2차 미분 방정식의 다른 예를 들어봅시다. y" - y = 0, y(0) = -1, y'(0) = 2.
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')
MATLAB은 코드를 실행하고 다음과 같은 결과를 반환합니다 -
ans =
exp(t)/2 - (3*exp(-t))/2'프로그래밍 > 매트랩' 카테고리의 다른 글
| 매트랩 다항식 Polynomials (0) | 2023.08.11 |
|---|---|
| 매트랩 적분 Integration (0) | 2023.08.10 |
| 매트랩 미적분학 Calculus (0) | 2023.08.10 |
| 매트랩 그래프 (플로팅) (0) | 2023.08.09 |
| 매트랩 데이터 타입 (0) | 2023.08.09 |