파형이 사이클당 최소 2개의 샘플을 제공하지 않는 주파수에서 샘플링될 때 정현파의 주파수 특성이 회복할 수 없을 정도로 손실된다는 것을 보았습니다. 즉, Nyquist 속도보다 낮은 주파수로 샘플링하는 경우 정현파를 완벽하게 재구성할 수 없습니다.
그러나 대부분의 신호는 단일 주파수 정현파가 아닙니다. 예를 들어, 변조된 RF 신호는 반송파 및 기저대역 파형과 관련된 주파수를 가지며, 인간의 음성을 나타내는 오디오 신호는 다양한 주파수를 커버합니다.
푸리에 변환을 사용하여 신호의 주파수 내용을 시각화합니다. 시간 영역 플롯은 단일 주파수 신호의 맥락에서 불충분한 샘플링 속도의 효과를 전달하는 좋은 방법이지만 다른 유형의 신호의 경우 주파수 영역을 사용하는 것이 좋습니다.
샘플링의 주파수 영역 효과
지정된 범위 내의 여러 주파수 혼합을 포함하는 오디오 신호를 디지털화하려고 합니다. 범위의 높은 끝을 fmax로 정의하고, 낮은 주파수는 들을 수 없지만 DC까지 범위가 확장된다고 가정합니다.
이러한 신호의 푸리에 변환은 다음과 같이 보일 수 있습니다:

시간 영역에서의 수학적 샘플링
수학적 영역에서 이상적인 샘플링은 원래의 시간 영역 파형에 1/fSAMPLE과 같은 간격으로 분리된 일련의 델타 함수를 곱하는 것과 같으며 이를 Tsample이라고 합니다. 이 곱셈으로 인해 샘플링된 신호는 델타 함수 사이에서 0이 되고 델타 함수와 일치하는 각 시점에서 원래 신호의 값을 유지하게 됩니다.

수학적으로 구현된 시간 영역 샘플링: 샘플링 주파수에서 발생하는 일련의 델타 함수로 아날로그 신호를 곱합니다.
주파수 영역에서의 수학적 샘플링
이 시간 영역 샘플링 절차는 신호의 주파수 영역 표현에 어떤 영향을 미치는지 확인해 봅시다.
가장 먼저 기억해야 할 것은 시간 영역에서의 곱셈이 주파수 영역에서 컨볼루션이 된다는 것입니다. 따라서 원래 신호의 푸리에 변환과 델타 함수의 푸리에 변환을 컨볼루션하여 샘플링된 신호의 푸리에 변환을 찾을 수 있습니다.
델타 함수 열차의 푸리에 변환은 델타 함수 열차라는 것이 밝혀졌습니다. 차이점은 델타 함수가 샘플링 기간이 아닌 샘플링 주파수에 해당하는 수평 거리로 분리된다는 것입니다.

샘플링 주기로 분리된 델타 함수 시퀀스의 스펙트럼은 샘플링 주파수로 분리된 델타 함수의 시퀀스입니다.
우리가 델타 함수의 스펙트럼을 원래 신호의 스펙트럼과 컨볼루션할 때, 우리는 델타 함수의 위치에 따라 이동하는 원래 스펙트럼의 복사본을 만듭니다. 따라서, 샘플링된 신호의 스펙트럼은 ±fS, ±2fS, ±3fS 등을 중심으로 하는 다수의 동일한 "하위 스펙트럼"으로 구성됩니다.

적절한 샘플링 주파수는 완전한 분리를 유지하기에 충분히 이동된 하위 스펙트럼을 생성합니다.
이제 주파수 영역 분석을 통해 Nyquist-Shannon 정리를 확인하는 데 필요한 정보가 있습니다.
시스템이 신호의 최고 주파수를 최소 2배 초과하는 속도로 아날로그 신호를 균일하게 샘플링하면 샘플링을 통해 생성된 이산 값에서 원래 아날로그 신호를 완벽하게 복구할 수 있습니다.
푸리에 변환의 음-주파수 부분 때문에, 원래 신호의 전체 수학적 대역폭은 2fmax입니다. 따라서, 서브스펙트럼이 겹치지 않도록 하기 위해서는 적어도 2fmax만큼 서브스펙트럼을 이동시켜야 합니다. 즉, 샘플링 주파수는 신호의 최대 주파수보다 적어도 2배 이상 높아야 합니다.
이 조건이 충족되면 원래 신호를 완벽하게 복원할 수 있습니다. 원래 스펙트럼이 변경되지 않았고 저역 통과 필터링을 통해 다른 하위 스펙트럼을 제거할 수 있기 때문입니다. 조건이 충족되지 않으면 하위 스펙트럼이 중첩되고 원래 스펙트럼이 변경되며 아무리 저역 통과 필터링을 해도 원래 신호가 복원되지 않습니다.
앨리어싱
하위 스펙트럼 겹침은 Nyquist 속도보다 낮은 샘플링 주파수를 사용할 때 정보가 손상되는 이유입니다. 하위 스펙트럼의 겹치는 부분은 추가를 통해 결합됩니다. 저역 통과 필터를 사용하여 원래 스펙트럼을 분리하려고 하면 중첩 대역의 주파수 성분이 달라지고 결과적으로 해당 시간 영역 신호가 달라집니다.
이에 대한 공식 명칭은 앨리어싱입니다.
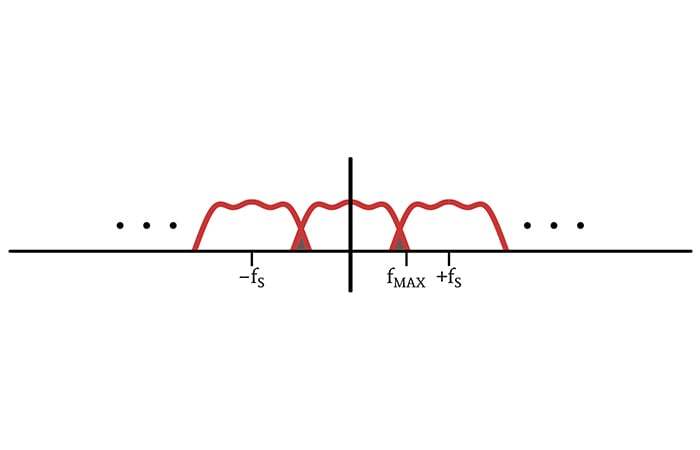
갈색으로 음영 처리된 삼각형 영역은 스펙트럼 변화를 일으킨 앨리어싱을 나타냅니다.
명사 "alias"의 정의 중 하나는 "거짓 또는 가정된 동일성"입니다. 이 샘플링 현상이 하나의 주파수 성분이 스펙트럼의 새로운 위치로 이동하여 다른 주파수로 "변장"할 수 있기 때문에 "aliasing"이라는 용어를 사용합니다.
1.1fsignal에서 샘플링한 결과 이산 시간 파형이 원래 아날로그 파형의 주파수보다 훨씬 낮은 주파수를 갖는 것으로 나타났습니다.
'데이터계측분석 > 데이터계측 기술자료' 카테고리의 다른 글
| 음향방출시험의 방법과 표준 (0) | 2024.10.29 |
|---|---|
| 계측데이터의 비선형성 처리방법 (0) | 2024.08.29 |
| 나이퀴스트 이론 - 샘플링 (0) | 2023.09.13 |
| 측정 노이즈 제거 팁 (0) | 2023.09.12 |
| 데이터 수집 시스템의 원리 (0) | 2023.07.18 |