숫자의 표현을 "숫자 체계" 또는 "숫자 체계"라고 합니다. 디지털 전자 제품의 관점에서 숫자 체계는 'Binary', 'Octal', 'Hexadecimal', 'Decimal'등과 같은 많은 유형입니다.
십진수 체계
이것은 우리가 일상 생활에서 사용하는 숫자 체계입니다. 이 시스템에서는 숫자의 위치를 단위, 수십, 수백, 수천 등으로 간주합니다. 소수점을 기준으로 한 숫자의 위치에 따라 값이 결정됩니다. 십진수의 밑은 10입니다. 다음과 같이 십진법으로 숫자를 계산해 보겠습니다.

여기서 가장 왼쪽 비트는 "최상위 비트" 또는 "MSB"라고 하고 가장 오른쪽 비트는 "최하위 비트" 또는 "LSB"라고 합니다.
또 다른 예를 살펴 보겠습니다.

이진수 체계
이진수 체계는 0과 1의 두 자리 숫자만 사용합니다. 위치 숫자 시스템으로, 이는 위치가 2의 거듭제곱으로 가중치가 부여됨을 의미합니다. 대부분 바이너리 시스템은 디지털 시스템에서 사용됩니다.
컴퓨터에 대한 데이터는 이진수 0과 1의 형식이어야 합니다.

이진수 체계를 이해하기 위한 예
21은 이진계에서 10101로 표현된다2 = 1 × 24 + 0 × 23 + 1 × 22 + 0 ×21 + 1 ×20 = 16 + 4 + 1 = 21
23은 이진계에서 10111로 표현된다2 = 1 × 24 + 0 × 23 + 1 × 22 + 1 × 21 + 1 × 20 = 16 + 4 + 2 + 1 = 23
35은 이진계에서 100011로 표현된다2 = 1 × 25 + 0 × 24 + 0 × 23 + 0 × 22 + 1 × 21 + 1 × 20 = 32 + 2 + 1 = 35
0 또는 1은 'BIT'로 호출됩니다. NIBBLE'은 4비트의 조합입니다. 'BYTE'는 8비트의 조합입니다.
일반적으로 메모리 크기를 바이트 단위로 측정합니다.
이진수에서 10진수로의 변환
2가지 방법으로 이진수를 십진수로 변환할 수 있습니다.
1. 각 이진수에 위치 값 곱하기
오른쪽에서 계산하면 가장 오른쪽 비트의 값은 1, 다음 비트의 값은 2, 다음 비트의 값은 4, 다음 비트의 값은 8 등입니다.
예를 들어 1011을 십진수로 변환합니다

2. 2씩 나누기를 반복한다
십진수를 이진수로 변환하는 잘 알려져 있고 쉬운 방법은 "2로 반복 나누기"입니다.
정수를 한 밑에서 다른 밑으로 변환하는 방법을 "반복 나눗셈"이라고 합니다. 십진수를 기본 숫자로 나누면 "Reminder"라는 몫이 생깁니다.
알림은 첫 번째 이진수로 기록되고 몫은 다시 기본 숫자로 나뉘므로 두 번째 몫과 두 번째 알림이 표시됩니다. 이것은 두 번째 이진수로 기록되며 이 과정은 몫이 0이 될 때까지 계속됩니다.
이런 식으로 십진수를 2로 나누면 알림은 0 또는 1입니다. 이진 결과는 첫 번째 알림을 '최하위 비트'로 작성하고 마지막 알림을 '최상위 비트'로 작성하여 얻습니다.

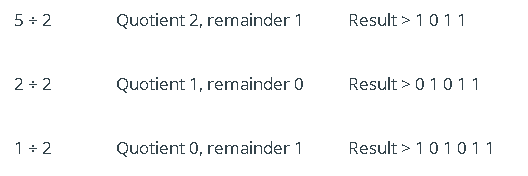


이진수 표현
우리는 십진법이 10진수로 표시된다는 것을 이미 알고 있습니다. 이것은 (왼쪽부터 시작하는) 각 자릿수의 가중치가 10배 증가한다는 것을 의미합니다. 마찬가지로 모든 이진 숫자는 기본 2로 표시되므로 각 숫자의 가중치(왼쪽부터 시작)가 2배 증가합니다. 즉, 첫 번째 숫자는 20, 두 번째 숫자는 21로 표시됩니다.
이를 명확하게 이해하려면 아래 그림을 참조하십시오.

이진수 이름 및 접두사
숫자 이름
이진수는 또한 덧셈과 뺄셈과 같은 수학 연산을 수행합니다. 따라서 덧셈과 뺄셈에서 십진수는 이진수 그룹(0 & 1)으로 표시됩니다. 기본적으로 이진수 그룹은 3가지 형태로 알려져 있습니다.
Bit, Byte 및 Word입니다.
0 또는 1을 '비트'라고 합니다.
4비트를 '니블'이라고 합니다.
8 비트 또는 2 니블은 '바이트'로 호출됩니다.
16 비트 또는 4 니블 또는 2 바이트를 'Word'라고합니다.
32 비트 또는 8 니블 또는 4 바이트 또는 2 단어를 'Double'이라고합니다.
64 비트 또는 16 니블 또는 8 바이트 또는 4 단어 또는 2 더블을 '쿼드'라고합니다.
숫자 접두사
디지털 시스템의 데이터/정보를 하나의 표기법에서 다른 표기법(이진법에서 십진법으로, 십진법에서 십진법으로, 십진법에서 이진법으로)으로 변환하는 동안, 우리는 두 표기법 중 하나만 따라야 합니다. 데이터가 한 표기법에서 다른 표기법으로 다를 수 있기 때문입니다. 예를 들어, "10"이라고 말할 경우 10진수로 "10"으로 표시되며 이진법 표기법으로 "1"과 "0"(숫자 2와 동일)으로 보일 수 있습니다.
숫자나 숫자 끝에 첨자를 적으면 이 문제를 극복할 수 있습니다. 이 첨자를 "접두사"라고 합니다. 예를 들어, 이진 시스템에서 숫자를 표현하는 경우 (1101011)2로, 십진수 시스템에서는 (432)10으로, 헥사 십진수 시스템 표현에서는 (480)hex로 표현해야 합니다.
오늘날에는 디지털 전자 세계가 빠르게 발전하고 있으며 숫자 표현은 새로운 방식을 가지고 있습니다. 비트(가장 작은 것)에서 요타바이트(가장 큰 것)까지 매우 다양합니다.
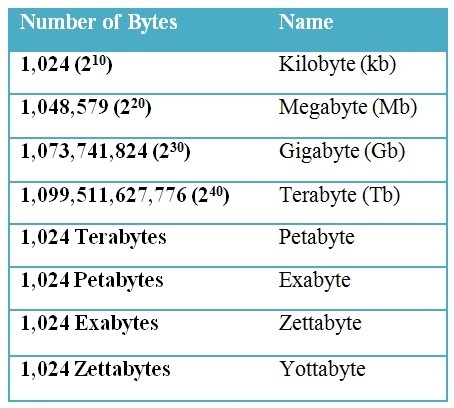
일반적으로 테라바이트를 가장 높은 크기의 메모리 측정으로 사용합니다.
- "Binary Digit"이라는 단어를 "BIT"라고 합니다.
- 십진법은 정기적으로 숫자를 나타내는 데 사용하는 것입니다.
- 십진법에서 숫자는 밑수 10으로 표시됩니다. 예: (432)10
- 이진수 시스템 또는 이진수 시스템에는 두 자리 숫자(0과 1)만 있습니다.
- 이진수는 왼쪽에서 오른쪽으로 2의 거듭제곱으로 가중치가 부여됩니다.
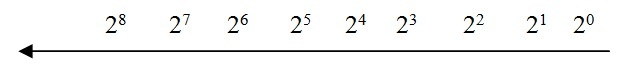
- 십진수를 이진수로 변환하는 방법에는 두 가지가 있습니다.
- 가중치의 합 방법.
- 2로 반복 나눗셈.
- 숫자를 이진수에서 십진수로 또는 십진수에서 이진수로 변환하는 동안 숫자를 나타내는 숫자 체계의 유형을 이해하는 데 오류가 발생하지 않도록 접두사 표기법을 따릅니다.
- 이진수는 Bit, Nibble, Byte, Word 등과 같은 많은 이름으로 표현됩니다. 비트가 가장 작고 테라바이트가 가장 높습니다.
'데이터계측분석 > 전기전자 기술자료' 카테고리의 다른 글
| DC 모터 - 직류 전동기 (0) | 2023.07.26 |
|---|---|
| 16진수 Hexadecimal (0) | 2023.07.20 |
| 바이너리 코드 - BCD (8421), 2421, Excess-3, Gray (0) | 2023.07.20 |
| 전자기계 릴레이 (0) | 2023.07.19 |
| 전기 배선 기호의 의미와 기능 (0) | 2023.07.19 |