인코더는 친숙한 숫자, 문자 또는 기호를 코딩된 형식으로 변환하는 장치입니다. 알파벳 문자와 10진수를 입력으로 받아들이고 입력을 코드화된 표현으로 생성합니다.
주어진 정보를 보다 간결한 형태로 인코딩합니다. 즉, 디코더의 반대 기능을 수행하는 조합 회로입니다.
이들은 주로 주어진 정보를 표현하는 데 필요한 비트 수를 줄이는 데 사용됩니다. 디지털 시스템에서 인코더는 정보를 전송하는 데 사용됩니다. 따라서 전송 링크는 인코딩된 정보를 전송하기 위해 더 적은 수의 라인을 사용합니다.
바이너리 인코더
바이너리 인코더에는 2n 개의 입력 라인과 n 개의 출력 라인이 있으므로 2n 개의 입력에서 n 비트 코드로 정보를 인코딩합니다. 모든 입력 라인에서 한 번에 하나의 입력 라인만 활성화되며 입력 라인에 따라 n 비트 출력 코드를 생성합니다.
아래 그림은 2n 개의 입력 라인과 n 개의 출력 라인으로 구성된 바이너리 인코더의 블록 다이어그램을 보여줍니다. 십진수를 이진수로 변환합니다.
인코더의 출력 줄은 입력 값에 해당하는 실제 이진 또는 BCD 코드 형식의 이진 값에 해당합니다. 이러한 이진 인코더 중 일부에는 10진수에서 이진 인코더, 10진수에서 8진수, 8진수에서 이진 인코더, 10진수에서 BCD 인코더 등이 포함됩니다.
입력 라인의 수에 따라 디지털 또는 바이너리 인코더는 2 또는 3 또는 4 비트 코드 형태로 출력 코드를 생성합니다.

4 – to – 2 Bit Binary Encoder
아래 그림에는 4개 입력 인코더의 블록 다이어그램과 진리 테이블이 나와 있습니다. 진리 테이블은 4개의 행으로 구성되어 있습니다. 왜냐하면, 하나의 입력만 1의 값이라고 가정하고, 그러면 해당 활성화된 입력과 관련된 해당 이진 코드가 출력에 표시되기 때문입니다.
표에서 관찰할 것은 입력 w1 또는 w3 중 하나가 1일 때 출력 Yo가 1이고 입력 w2 또는 w3 중 하나가 1일 때 출력 Y1이 1로 설정된다는 것입니다.

4-to-2 인코더의 출력은 아래와 같은 OR 게이트 세트로 구현된 논리 회로에 의해 생성됩니다. 그림 a에서 활성화된 입력이 Io 입력(Io = 1)이거나 활성화된 입력이 없는 경우, 즉 모든 입력이 0입니다.
이로 인해 인코딩 출력에 모호성이 발생합니다. 이러한 모호성을 방지하기 위해 유효한 인코딩 출력을 추가 출력으로 추가할 수 있으므로, 이 출력은 Io가 1과 같을 때 값 1을 가정합니다.

4 – to – 2 Bit Binary Encoder
이 유형의 인코더는 일반적으로 10개의 입력 라인과 4개의 출력 라인으로 구성됩니다. 각 입력 라인은 각 소수점 숫자에 해당하고 4개의 출력은 BCD 코드에 해당합니다.
이 인코더는 디코딩된 십진 데이터를 입력으로 받아 출력 라인에서 사용할 수 있는 BCD 출력으로 인코딩합니다.
아래 그림은 십진 대 BCD 인코더의 기본 논리 기호를 진리표와 함께 보여줍니다. 진리표는 각 십진 숫자에 대한 BCD 코드를 나타냅니다.
이로부터 우리는 BCD 비트와 십진 숫자 사이의 관계를 공식화할 수 있습니다. 십진 0에 대한 명시적인 입력 라인이 없다는 것을 유의해야 합니다. 이 조건이 발생할 때, 즉 십진 입력 1부터 9까지 모두 0이고, BCD 출력은 0000입니다.

위의 표에서 다음과 같은 표현식을 얻습니다.
Y3 = D8 + D9
Y2 = D4 + D5 + D6 + D7
Y1 = D2 + D3 + D6 + D7
Y0 = D1 + D3 + D5 + D7 + D9
위의 식에서 10진수에서 BCD 인코더 논리 회로는 아래 그림과 같이 OR 게이트 집합을 사용하여 구현할 수 있습니다.

Octal to Binary Encoder
8진수에서 2진수 인코더는 8개의 입력 라인과 3개의 출력 라인으로 구성됩니다. 각 입력 라인은 각 8진수에 해당하고 3개의 출력은 해당하는 2진수 코드를 생성합니다.
인코더에서, 하나의 입력만 활성이거나 주어진 시간에 값이 1인 것으로 가정해야 합니다. 그렇지 않으면 회로는 아무런 의미를 갖지 않습니다. 아래 그림은 8진수에서 2진수 인코더의 논리 기호를 진리 표와 함께 보여줍니다.

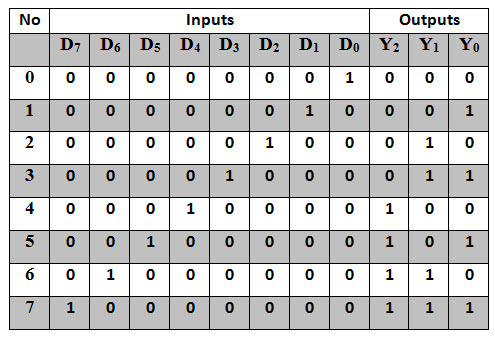
ㅊ위의 표에서, D4, D5, D6, D7 중 어느 하나의 숫자가 1이면 Y2 출력은 1이 됩니다. 따라서 그 표현을 다음과 같이 쓸 수 있습니다.
Y2 = D4 + D5 + D6 + D7
Y1 = D2 + D3 + D6 + D7 및 Y0 = D1 + D3 + D5 + D7
또한 D0는 어떤 식에도 존재하지 않으므로 상관없는 것으로 간주됩니다. 위의 식으로부터 아래 그림과 같이 OR 게이트 집합을 사용하여 8진 부호화기를 구현할 수 있습니다.

8진-이진 인코더에는 모든 입력이 0일 때 모든 0의 출력이 생성된다는 모호함이 있습니다. 또한 Do가 1일 때 생성되는 출력은 0입니다. 이것은 이러한 유형의 인코더에서 주요 문제입니다. 이것은 추가 출력으로 입력 중 아무 것도 활성화되지 않는다는 조건을 지정하여 해결할 수 있습니다.
디지털 인코더 응용 분야
인코더는 모든 디지털 시스템에 사용되는 매우 일반적인 전자 회로입니다. 포켓 계산기의 경우 덧셈, 뺄셈, 곱셈 등과 같은 이진 기능을 수행하기 위해 십진수 값을 이진수로 변환하는 데 사용됩니다.
이들은 또한 샤프트 엔코더와 리니어 엔코더로 분류되는 움직임에 대한 응답으로 디지털 신호를 생성하는 데 사용됩니다. 인코더의 키보드 응용 프로그램에 대해 간략하게 논의해 보겠습니다.
키보드 인코더
이 유형의 인코더 기능은 키보드에서 눌러진 영숫자 문자 키에 대응하는 이진 코드를 생성하는 것입니다. 아래 그림은 다이오드 행렬을 사용하여 BCD 코드의 10진수를 인코딩하는 데 사용되는 키보드 인코더를 보여줍니다. 이 회로에서는 BCD 데이터가 S-R 플립플롭에 저장됩니다.

십진수 중 하나에 해당하는 키를 누르면 선택된 다이오드가 양의 전압에 의해 순방향 바이어스되고 SR 플립플롭의 설정 및 리셋 단자에 연결됩니다. 다이오드 배열은 각 플립플롭이 4비트 BCD 코드를 생성하도록 설정되거나 재설정되는 방식으로 이루어집니다.
십진수 7에 해당하는 키를 누르면 Q4, Q2 및 Q1의 S 입력에 연결된 다이오드가 순방향 바이어스되고 Q8의 R 입력에 연결된 다이오드도 순방향 바이어스된다고 가정합니다. 따라서 출력 BCD 코드는 0111입니다.
인코더의 논리 다이어그램에서 각 S 및 R 입력의 다이오드 구성은 본질적으로 다이오드 OR 게이트임을 알 수 있습니다. 이 유형의 다이오드 매트릭스 인코더는 키보드를 사용자 데이터 인터페이스로 사용하는 많은 전자 장치의 인쇄 회로 기판에 사용됩니다.
'데이터계측분석 > 전기전자 기술자료' 카테고리의 다른 글
| 기본 전자 부품 (0) | 2023.08.01 |
|---|---|
| 유효, 무효 및 피상 전력 (0) | 2023.07.31 |
| AC 파형의 RMS 전압 (0) | 2023.07.29 |
| 고조파 - Harmonic Frequencies (0) | 2023.07.28 |
| 정현파 파형 (0) | 2023.07.27 |