많은 실제 회로에는 저항, 유도 및 용량 성 요소의 조합이 포함되어 있습니다. 이러한 요소는 전압 및 전류와 같은 전기 공급 매개변수 사이에 위상 변이를 일으킵니다.
전압 및 전류의 거동으로 인해, 특히 이러한 구성 요소에 종속될 때 전력량은 다른 형태로 제공됩니다.
AC 회로에서 전압 및 전류 진폭은 시간이 지남에 따라 지속적으로 변합니다. 전력은 전압에 전류를 곱한 값이므로 전류와 전압이 서로 정렬되면 최대화됩니다.
이는 전류 파형과 전압 파형의 영점과 최대점이 동시에 발생한다는 것을 의미한다. 이는 유용한 전력이라고 할 수 있다.
인덕터나 축전기 소자의 경우 전압과 전류 사이에 90도의 위상 변이가 존재한다. 따라서 전압이나 전류 중 어느 하나가 0의 값을 가질 때마다 전력은 0의 값을 가질 것이다.
이것은 소스가 전력을 생성하고 있음에도 불구하고 부하에서 작업이 수행되지 않기 때문에 바람직하지 않은 조건이다. 이 전력을 무효전력이라고 한다.
AC 회로의 전원
모든 전기 회로의 전력은 해당 회로의 전압 및 전류 값을 곱하여 얻을 수 있습니다. 이는 DC 및 AC 회로 모두에 적용됩니다.
즉, 전력 = (전류 값) x (전압 값)
P = V x I
전력은 와트 단위로 측정됩니다. 비선형 구성 요소가 없는 DC 회로 및 순수 AC 회로에서 전류 및 전압 파형은 '동상'입니다.
따라서 해당 회로의 모든 순간의 전력은 전압과 전류를 곱하여 얻습니다.
그러나 AC 회로의 경우에는 그렇지 않습니다 (위에서 언급했듯이 위상 변이의 존재).

AC 공급이 부하에 제공되는 위의 회로를 고려하십시오. 회로의 전압과 전류는 다음과 같이 주어집니다.
v = Vm sin ωt ⇒ v = √2 V sin ωt
i = Im sin ωt ⇒ i = √2 I sin (ωt ± φ)
여기서 V(=Vm/√2) 및 I(=Im/√2)는 각각 회로를 통해 흐르는 인가 전압 및 전류의 RMS 값입니다.
Φ는 전압과 전류의 위상차이며, + 기호는 선행 위상각을 나타내고 음수는 지연 위상각을 나타냅니다.
그런 다음 소스에 의해 부하에 전달되는 순간 전력은 다음과 같이 주어집니다.
p = vi = 2 VI sin wt sin (ωt ± φ)
= VI (cos φ – cos (2ωt ± φ)
p = VI cos φ (1 – cos 2wt) ± VI sin φ sin2wt
위의 거듭제곱 방정식은 두 가지 용어로 구성됩니다.
- VI cos φ에 비례하는 항으로, VI cos φ의 평균값 주위에서 맥동합니다.
- VI sin에 비례하는 항φ 공급 주파수의 두 배에서 맥동하여 사이클 동안 평균 0을 생성합니다.
따라서 AC 회로에는 3가지 형태의 전력이 있습니다.
- 유효 전력 또는 진정한 전력 또는 실제 전력
- 무효 전력
- 피상 전력
유효 전력
회로에서 소비되거나 유용한 작업을 수행하는 실제 전력량을 활성 또는 실제 전력이라고 합니다. 와트 단위로 측정되며 실제로 전력 시스템에서 KW(킬로와트) 및 MW(메가와트)로 측정됩니다.
문자 P(대문자)로 표시되며 p = VI cos φ의 평균값과 같습니다. 회로 또는 부하를 구동하는 전기 시스템의 원하는 결과입니다.
P = VI cos φ
무효 전력
위의 파생식에서 두 번째 항의 평균값은 0이므로 이 항에 의해 기여되는 거듭제곱은 0입니다. VI sin φ에 비례하는 구성 요소는 문자 Q로 표시되는 무효 전력이라고 합니다.
전력이지만 비활성 전력이므로 와트로 측정되지 않으므로 VAR(Volt-Amperes-Reactive)로 측정됩니다. 이 무효 전력의 값은 부하 역률에 따라 음수 또는 양수일 수 있습니다.
이는 유도성 부하가 무효 전력을 소비하는 반면 용량성 부하가 무효 전력을 생성하기 때문입니다.
Q = VI sin φ
무효 전력의 중요성
무효 전력은 회로 또는 라인에서 앞뒤로 이동하는 전체 전력 구성 요소 중 하나입니다. 그것은 양의 반주기 동안 소스에서 반응성 구성 요소로 계속 흐르고 음의 사이클 동안 소스에서 구성 요소로 계속 흐르는 시간에 대한 에너지 변화율이라고 할 수 있습니다. 따라서 부하에 의해 소비되지 않습니다.
정상적인 의미에서 이 가상의 전력은 전혀 전력이 아니라 전류의 무효 성분에 대한 전력과 같은 척도일 뿐입니다. 무효 전력량이 초과되면 역률이 크게 감소합니다. 이 낮은 역률은 운영 효율성 및 운영 비용 측면에서 바람직하지 않습니다.
또한 이 전원으로 인해 공급 장치에서 추가 전류를 끌어와 추가 손실과 장비의 더 큰 용량이 발생합니다. 그래서 이 힘은 농담으로 전력선의 콜레스테롤이라고 불렸습니다.
손실을 최소화하고 사용 가능한 장비의 용량을 늘리기 위해 유틸리티 회사는 VAR 보상 기술 또는 역률 보정 장비를 사용합니다. 일반적으로 이러한 반응 보상 기술은 부하 측에서 구현됩니다.
그러나 이 무효 전력은 변압기, AC 모터 등과 같은 유도 장치의 작동에 필요한 자기장을 생성하는 데 유용합니다. 또한 무거운 전원 공급 메커니즘의 전압을 조절하는 데 도움이 됩니다.
피상 전력
실제 또는 유효 전력과 무효 전력의 복잡한 조합을 피상 전력이라고 합니다. 위상각을 참조하지 않고 전압과 전류의 곱은 피상 전력을 제공합니다. 피상 전력은 전력 장비의 정격에 유용합니다.
전류의 제곱에 회로의 임피던스를 곱한 값으로도 표현할 수 있습니다. 문자 S로 표시되며 볼트-암페어(VA)로 측정되며 실제 단위에는 KVA(킬로 볼트-암페어) 및 MVA(메가 볼트-암페어)가 포함됩니다.
피상 전력 = RMS 전압 × RMS 전류
피상 전력, S = V × I
복소수 형태에서 S = V I*
S = V ∠00 I ∠ φ(지연 부하 전류용)
S = V I ∠ φ
S = V I cos φ + jV I sine φ
S= P + jQ
또는 S = I^2Z
파워 트라이앵글
능동 전력, 무효 전력, 피상 전력의 관계는 수량을 벡터로 표현하여 표현할 수 있으며, 이는 아래와 같이 전력 삼각형 방법이라고도 합니다. 이 페이저 다이어그램에서 전압은 참조 벡터로 간주됩니다. 전압 및 전류 페이저 다이어그램은 전력 삼각형 형성의 기초입니다.

그림 (a)에서 전류는 각도 φ만큼 인가 전압보다 지연됩니다. 전류의 수평 성분은 I cos φ이고 전류의 수직 성분은 I sin φ입니다. 각 전류 페이저에 전압 V를 곱하면 그림 (b)와 같이 전력 삼각형이 얻어집니다.
유효 전력은 전압과 위상이 φ 성분 I cos에 의해 기여되는 반면 무효 전력은 직교 성분에 의해 생성됩니다.
따라서 삼각형의 피상 전력 또는 빗변은 실수 전력과 무효 전력을 벡터적으로 결합하여 얻습니다.
피타고라스의 정리를 사용하면 인접한 두 변의 제곱합(유효 전력과 무효 전력)은 대각선의 제곱(피상 전력)과 같습니다. 즉,
(피상 전력)2= (실제 힘)2
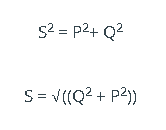
S = 킬로볼트 암페어, kVA로 측정된 피상 전력
Q = 킬로볼트 암페어 무효, kVAR로 측정된 무효 전력
P = 킬로와트, kW로 측정된 유효 전력
저항성, 유도성 및 임피던스 소자의 관점에서 전력 형태는 다음과 같이 표현할 수 있습니다.

X는 인덕턴스입니다.
Z는 임피던스입니다.
역률
역률은 전압과 전류 사이의 코사인 각도입니다. 역률은 위에서 논의한 전력 형태로 표현할 수 있습니다. 위 그림의 거듭제곱 삼각형을 생각해 보면 역률은 피상 전력에 대한 유효 전력의 비율입니다.
역률은 회로의 효율을 정의합니다.
역률(PF) = (와트 단위의 유효 전력)/(볼트 암페어 단위의 피상 전력)
PF = VI cos φ / VI
PF = cos φ
예제 문제
100V, 50Hz의 AC 전원 공급 장치가 임피던스 부하, 20 + j15 Ohms에 연결된 경우. 그런 다음 회로를 통해 흐르는 전류, 유효 전력, 피상 전력, 무효 전력 및 역률을 계산합니다.
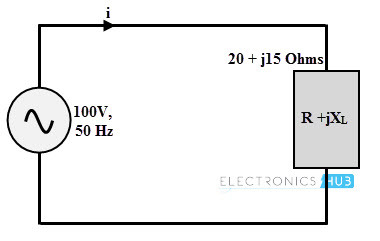
이를 감안할 때 Z = R + jXL = 20 + j 15 Ω
임피던스를 극성 형태로 변환하면 다음과 같은 결과를 얻을 수 있습니다.
Z = 25 ∠36.87 Ω
회로를 통해 흐르는 전류,
I = V/Z = 100∠00 /25 ∠36.87
I = 4 ∠–36.87
유효 전력, P = I^2R = 42 × 20 = 320와트
또는 P = VI cos φ = 100 × 4 × cos (36.87) = 320.04 ≈ 320W
피상 전력, S = VI = 100 × 4 = 400 VA
무효 전력, Q = √ (S2 – P2)
= √ (4002 – 3202) = 240VAr
역률, PF = cos φ = cos 36.87 = 0.80 지연.
'데이터계측분석 > 전기전자 기술자료' 카테고리의 다른 글
| 이더넷 케이블 RJ45 핀아웃(Cat 5e, 6 및 7) (0) | 2023.09.07 |
|---|---|
| 기본 전자 부품 (0) | 2023.08.01 |
| 바이너리 인코더 (0) | 2023.07.29 |
| AC 파형의 RMS 전압 (0) | 2023.07.29 |
| 고조파 - Harmonic Frequencies (0) | 2023.07.28 |