수학적 계산에 사용되는 숫자는 부호가 양수 또는 음수입니다. 양수는 일반적으로 부호가 없으며 양수(+) 기호가 없습니다. 또한 부호가 없는 숫자는 양수로 이해됩니다. 이와 반대로 음수는 숫자의 가장 왼쪽에 음수 기호(-)로 표시되는 부호 있는 숫자입니다
이진수는 부호 없는 이진수, 즉 양수 값뿐입니다. 디지털 시스템과 컴퓨터의 아키텍처는 이진수만 이해하기 때문에 실제 부호를 양수(+) 또는 음수(-) 기호로 이진수로 표현하는 것은 불가능합니다. 이진수는 "0" 또는 "1"의 값을 가질 수 있는 이진수(비트)로 표시되기 때문에, 즉 비트를 나타내는 숫자는 두 개만 가질 수 있습니다. 비트 값 "0" 또는 "1"은 디지털 회로에 의존하는 로직 레벨의 단순한 표현입니다. 즉, "0"과 "1" 이외의 다른 숫자에 대한 표현과 이해는 디지털 시스템의 하드웨어 수준에서 불가능합니다. <>진수와 달리 음수 값을 나타내기 위해 이진수와 함께 음수 부호를 포함할 수 없습니다.
부호 및 크기
숫자는 본질적으로 양수와 음수 값을 나타내기 위해 부호와 크기의 두 가지 값을 가져야 합니다. 이 표현을 SM(Sign-and-Magnitude) 표기법이라고 합니다. 예를 들어 음수(-12345)는 이 SM(Sign-and-Magnitude) 표기법을 사용하여 표시됩니다. Sign-and-Magnitude 메서드는 양수와 음수를 모두 나타내는 가장 간단하고 가장 일반적으로 사용되는 방법입니다. Sign-and-Magnitude 방법은 음수와 양수를 나타내기 위해 이진수에도 적용할 수 있습니다. 크기와 함께 부호(양수 또는 음수 값)를 갖는 이진수를 부호 있는 이진수라고 합니다.
이진수는 "0" & "1"로만 표시되며 Sign-and-Magnitude 표기법을 사용하기 위해 (+) 또는 (-) 기호를 포함하는 조항은 없습니다. 이 Sign-and-Magnitude 방법을 채택하기 위해 MSB(최상위 비트)는 이진수의 양수 또는 음수 값을 나타내는 부호로 사용됩니다. 부호 있는 양의 이진수 "0"을 나타내는 데 가장 중요한 비트로 사용되는 반면 "1"은 음의 부호 있는 이진수를 나타냅니다. 이 부호 및 크기 표기법을 사용하면 부호 있는 이진수의 최상위 비트는 부호(양수 또는 음수 표기법)를 보유하고, 나머지 비트는 부호 있는 이진수의 크기 또는 값을 나타냅니다.
"n"비트 수를 가지는 부호화된 이진수는 부호를 나타내기 위해 1비트를 사용하고 크기 또는 값을 나타내기 위해 "n-1"비트를 사용합니다. 부호와 크기 표기법을 사용하면 십진수 (45)의 양수와 음수를 부호화된 이진수로 나타낼 수 있습니다. 십진수는 앞의 글에서 설명한 2등분 반복법을 사용하여 이진수로 변환할 수 있습니다.
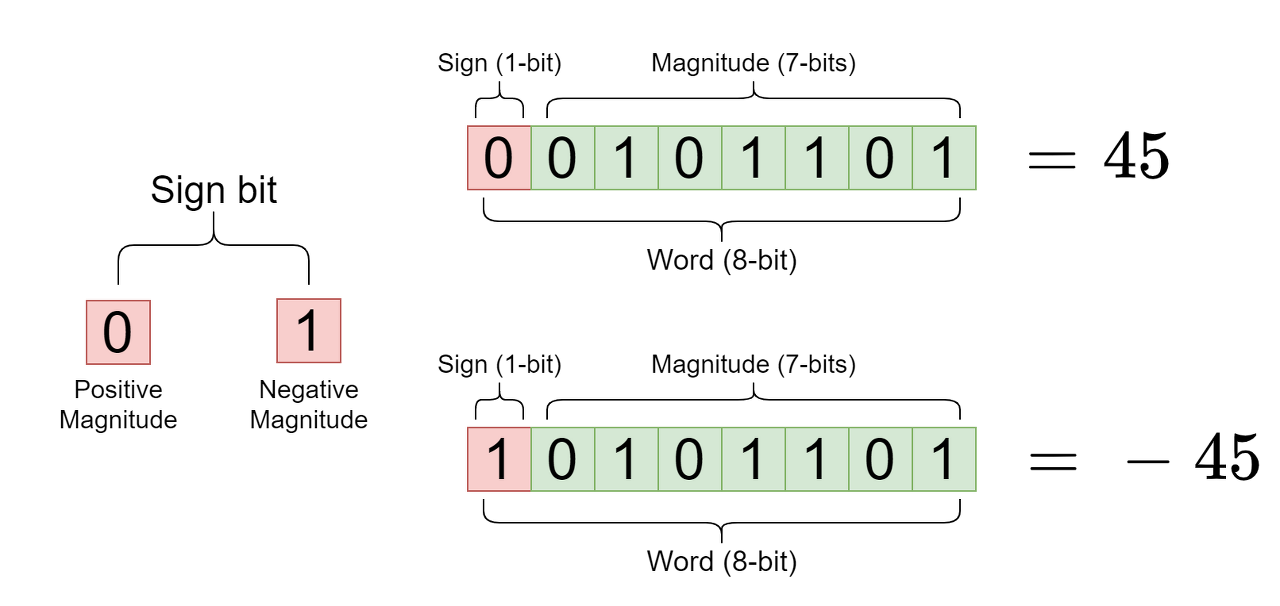
그러나 Sign-and-Magnitude 표기법에는 여러 가지 단점이 있습니다. 1비트를 부호 비트로 사용하면 크기 또는 값을 보유하는 비트 수가 줄어듭니다. "n"개의 비트를 갖는 부호 없는 이진수와 비교할 때, 부호 있는 이진수는 값을 나타내기 위해 "n-1" 비트를 갖게 됩니다. 부호 및 크기 표기법은 숫자 값을 두 개의 반쪽, 즉 영(0)의 양쪽에 하나씩 분할합니다. 이를 이해하기 위해 부호 없는 이진수와 부호 있는 이진수의 십진수 범위는 다음과 같습니다. 부호 없는 숫자와 부호 있는 숫자의 크기는 모두 8비트로 설정됩니다.

8비트 부호 없는 숫자의 숫자 범위는 "0"에서 "255"까지, 즉 표현할 수 있는 총 256개의 숫자입니다. 반면 부호 있는 이진수의 범위는 "-127"에서 "127"까지이며 중간 값 "0"을 포함합니다. 부호 있는 숫자로 표시되는 값의 개수는 "255"입니다. 마찬가지로, 부호가 없는 4비트 이진수의 10진수 범위는 다음과 같습니다:

마찬가지로, 부호 없는 4비트 이진수와 부호 있는 이진수의 범위는 각각 (0 ~ 15 = 16)과 (-7 ~ +7 = 15)입니다. 여기서도, 부호와 크기 표기는 동일한 부호 없는 이진수에 비해 값의 수를 1만큼 줄였습니다.
게다가, 부호와 크기 표기에는 각각 양과 음의 0을 나타내는 두 개의 0 값이 있습니다. 예를 들어, "0" 값으로 배치된 "0"의 부호 비트는 양의 0, 즉 00002를 보여줍니다. 마찬가지로, "0" 값으로 배치된 "1"의 부호 비트는 음의 0, 즉 10002를 보여줍니다. 부호와 크기 표기에 따르면, 둘 다 유효하고 이것은 위에서 논의한 숫자 값 중 하나를 차지합니다.
부호 있는 이진수 예제
다음 표에는 양수와 음수를 같은 부호의 이진수로 표현하는 예제가 많이 나와 있습니다. 십진법에서 이진법으로의 변환은 반복 나눗셈 by 2 방법을 적용하여 이루어집니다.
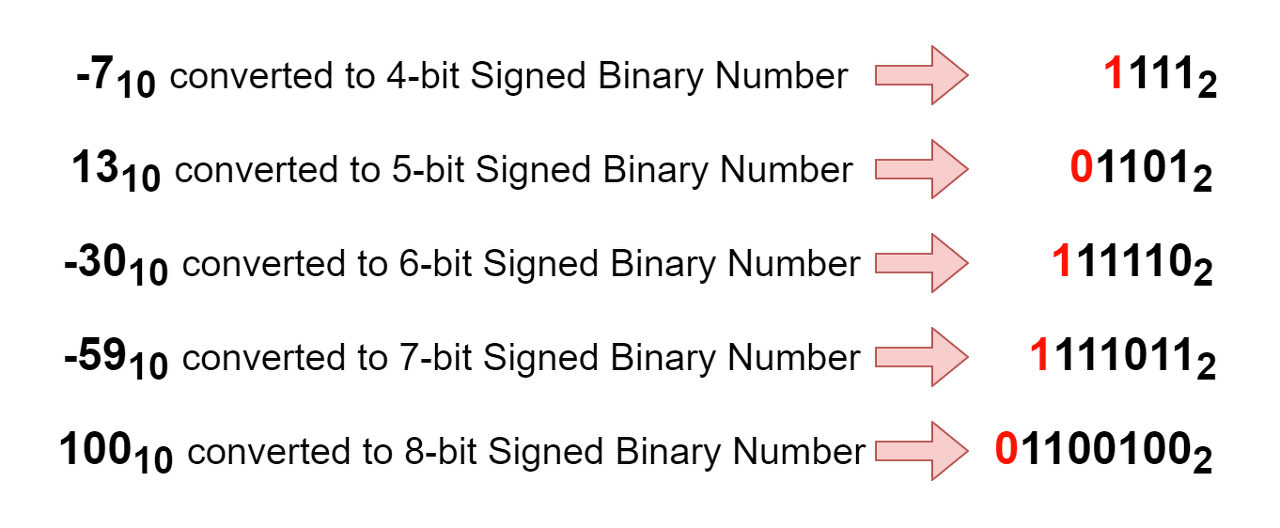
부호 및 크기 표기법을 사용하기 위해 부호 비트는 최상위 비트(MSB)에 배치되는 반면 나머지 비트는 크기 또는 값을 나타냅니다. 크기 또는 값이 더 작고 크기 비트를 모두 차지하지 않으면 나머지 크기 비트는 영(0)으로 설정됩니다. 이 배열은 부호 비트의 위치(예: 8비트, 16비트 또는 32비트 등의 MSB)를 식별하는 데 도움이 됩니다.
1의 보수
1의 보수는 부호 있는 이진수의 음수를 나타내는 또 다른 방법입니다. 양수 값은 변경되지 않은 상태로 유지되므로 보완되지 않은 값이라고 합니다. 양수 값은 부호 및 크기 양수 값에 대해 표시된 값과 동일합니다. 그러나 음수 값은 반전되거나 부정되는 보수입니다. 예를 들어, "0"의 보수는 "1"이고 "1"의 보수는 "0"입니다. 따라서 주어진 양의 부호 있는 이진수의 음수는 보수를 취하거나 "0"을 "1"로 또는 그 반대로 변경하여 결정할 수 있습니다.
예를 들어, 101100112의 1보수는 010011002입니다. 디지털 회로나 논리 회로에서는 "Inverters"를 사용하여 1보수를 달성합니다. 필요한 병렬 인버터의 수는 부호화된 이진수(비트 수)의 크기나 길이에 따라 달라집니다.
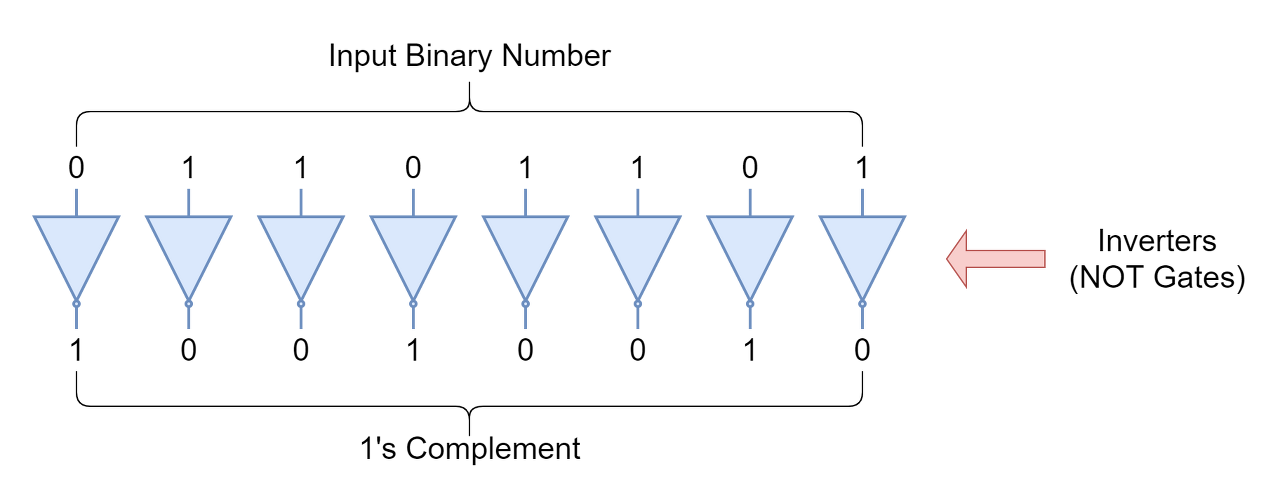
부호 및 크기 표기법과 유사하게 보어는 -(2n-1-1)에서 -(2n-1-1) 사이의 n비트 표기법을 가지며 4비트 부호가 있는 숫자의 경우 0을 나타내는 00002(양수)와 11112(음수)의 두 가지 값을 가집니다.
1의 보수를 이용한 덧셈과 뺄셈
두 개의 2진수의 덧셈은 이진수를 뺄 때 사용할 수 있습니다. 두 개의 2진수의 덧셈은 가산 회로를 사용하여 합과 캐리 비트가 생성됩니다. 덧셈 결과는 입력된 값의 값에 따라 달라집니다. 수학에서, 숫자의 뺄셈은 뺄셈 피연산자를 더하기 위해 반전된 두 숫자를 더한 A + (-B)로 공식화할 수 있습니다. 이 공식을 사용하여 두 개의 2진수의 뺄셈은 원하는 피연산자에 대한 곱셈을 사용하여 수행할 수 있습니다.
예를 들어, 수학식 108 – 45 = 63은 1의 곱셈을 사용하여 수행됩니다. 십진수는 동등한 십진수로 변환되고 두 개의 2진수 모두 선행 0을 더하여 8비트로 조정됩니다.
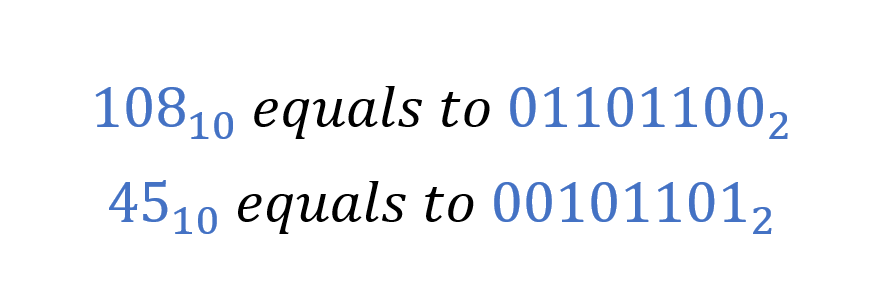
덧셈이나 덧셈을 이용하여 10810에서 4510을 빼기 위해, 4510의 보어는 매 비트를 반전시켜 결정됩니다. 4510의 동치 이진수는 001011012이고 보어는 110100102입니다. 이제 10810 = 011011002에 보어를 더하면 다음과 같이 보어를 뺄 수 있습니다.

위의 결과에서 9일 bit는 오버플로 비트이며 빼기 결과가 양수임을 나타냅니다. 빼기로 인해 오버플로 비트가 없으면 결과는 음수입니다. 따라서 이 오버플로의 경우 9일 bit 또는 overflow bit는 무시해도 됩니다. 이제 이 보완된 결과를 실제 결과로 변환하기 위해 아래와 같이 "1"이 추가됩니다.

보수를 이용하여 뺄셈을 하면 6310이 되는 결과(0011112)가 나옵니다. (0011112)의 등가 십진수는 가중치가 부여된 곱의 합, 즉 (32+16+8+4+2+1) = 63으로 결정됩니다. 따라서 보어를 이용하면 74LS83, 74LS283 등과 같은 이진법 덧셈기에서 부호가 부여된 이진법을 뺄 수 있습니다.
2의 보수
2의 보수는 부호화된 이진수 체계에서 음수를 나타내는 또 다른 방법입니다. 부호화와 크기화 방법과 1의 보수처럼, 양의 이진수는 변하지 않습니다. 반면에 2의 보수에서 음수는 최하위 비트(LSB)에 대한 하나의 보법 플러스(+) "1"입니다. 상대 양수에 더해질 때 음의 이진수는 0이 됩니다. 2의 보수는 부호화와 크기화 방법에서 관찰되었던 이중 0 문제를 포함하지 않습니다. 게다가, 산술 연산을 상대적으로 훨씬 더 쉽게 만드는 둘의 보법을 구하는 것이 훨씬 더 쉽습니다.
2의 보수 부호화된 이진수의 범위는 아래에 주어집니다.
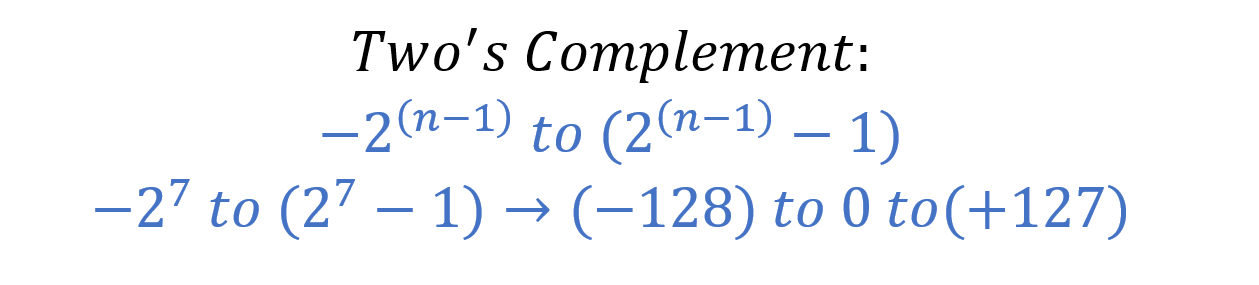
앞의 보어 예를 사용하면, (4510 = 001011012)의 보어는 먼저 보수를 구하고 여기에 "1"을 더하면 얻어집니다. (110100102 + 000000012 = 110100112).
2의 보수 4510은 부호가 있는 이진수에서 -4510과 같습니다. 따라서 뺄셈 (10810 – 4510)은 아래와 같이 부호가 있는 이진수를 모두 더하면 얻어집니다.

오버플로 비트는 삭제되고 나머지 8비트는 (6310 = 32+16+8+4+2+1)입니다.
다음 표에서는 부호 있는 4비트 이진수를 나타내는 여러 가지 방법을 비교한 것입니다.
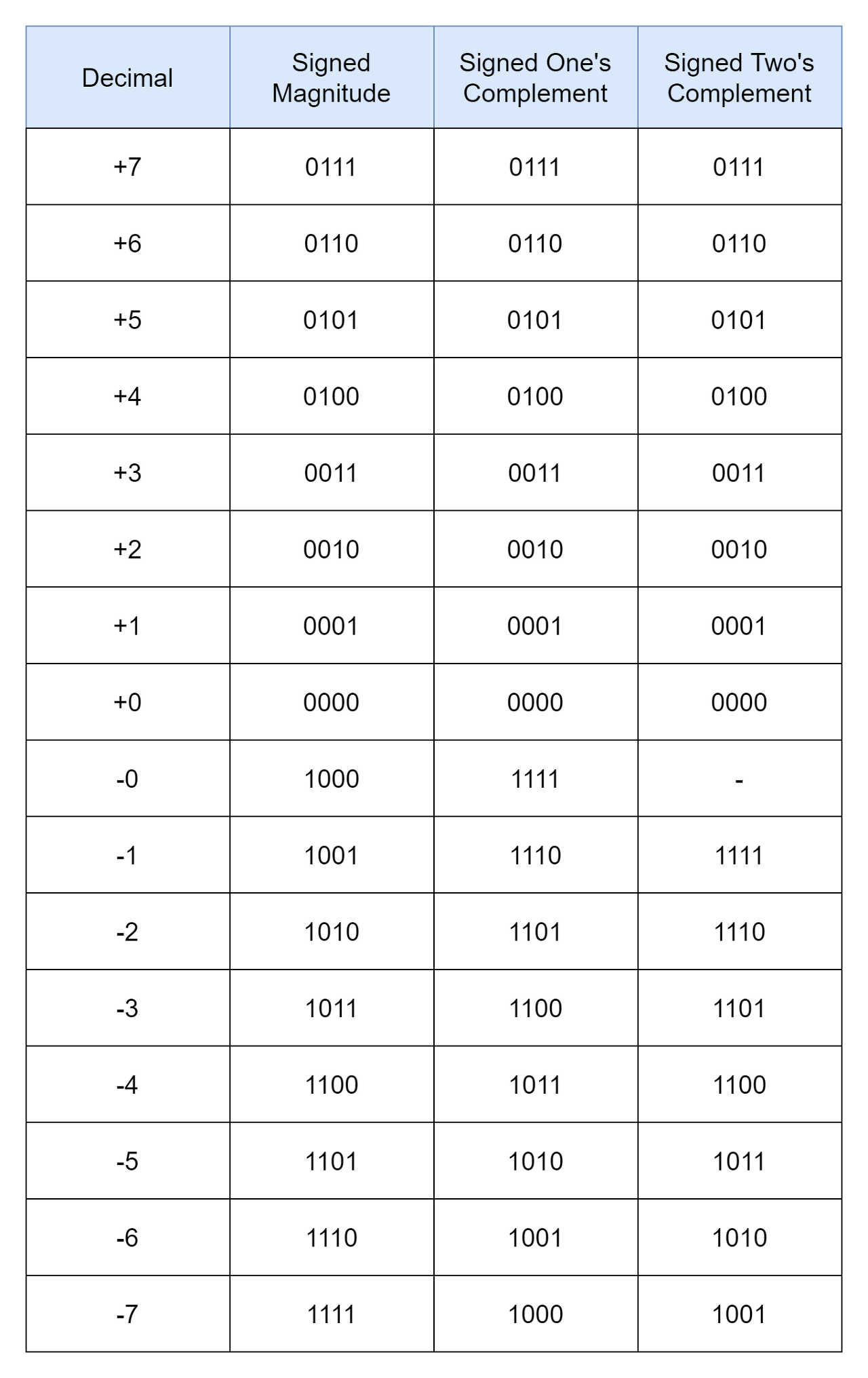
부호화된 이진수 체계는 이진수에서 양수와 음수를 모두 나타내는 데 사용됩니다. 부호화된 이진수를 나타내는 데 사용되는 방법은 부호화 크기(Sign-and Magnitude), 1의 보수(One's Complement), 2의 보수(Two's Complement)입니다.
부호화 크기(Sign-and Magnitude)는 부호 비트로 가장 유의한 비트(MSB)를 사용합니다. 0(0)은 양의 크기를 나타내고 1(1)은 이진수의 음의 크기를 나타냅니다. 숫자의 범위는 -127에서 -0, +0에서 +127로 나뉩니다. 부호화된 이진수는 부호화 크기(Sign-and Magnitude)와 마찬가지로 부호화된 이진수와 부호화된 이진수를 나타냅니다.
부호화 크기(Sign-and Magnitude)는 부호화 크기(Sign-and Magnitude)와 1의 보수(One's Complement) 방법과 마찬가지로 양수가 변하지 않습니다. 음수는 먼저 해당 양수의 1의 보수를 결정한 후 "1"을 더하면 얻어집니다. 숫자의 범위는 -128에서 0까지이고 범위에 오직 하나의 0만 포함합니다. 두 개의 상보법은 제시된 다른 방법에 비해 부호화된 이진수를 나타내는 데 가장 일반적으로 사용되는 방법입니다. 두 개의 상보법의 사용은 이중 0의 문제를 피하고 산술 연산이 비교적 훨씬 쉬워집니다.
'데이터계측분석 > 전기전자 기술자료' 카테고리의 다른 글
| 7세그먼트 디스플레이 디코더 (0) | 2023.09.14 |
|---|---|
| 스위치 동작방식과 이론 (0) | 2023.09.14 |
| 하모닉스 - 고조파 (0) | 2023.09.14 |
| AC회로의 평균 및 RMS 전압 (0) | 2023.09.13 |
| 셀렉터 스위치 (0) | 2023.09.13 |