스위칭 이론은 디지털 로직 게이트 및 회로의 작동 및 기능을 이해하기 위해 스위치를 사용합니다. 스위칭 이론은 특정 관계형 논리 출력을 생성하는 논리 입력을 포함하는 디지털 논리 회로에 대한 더 나은 이론적 지식과 개념을 개발하는 데 도움이 됩니다. 이미 논의 된 바와 같이, Boolean 데이터 유형에는 "0"또는 "1"이라는 두 가지 고유 한 상태 만 있습니다.
각각 "LOW" 및 "HIGH" 또는 "OFF" 및 "ON"이라고도 합니다. 디지털 로직 입력 및 출력은 이 두 가지 상태만 가질 수 있습니다. 계전기의 스위치 또는 전기 기계 접점에는 "OFF" 또는 "ON"이라는 두 가지 고유한 상태만 있습니다. 따라서 디지털 논리 입력 또는 출력은 물리적 스위치로 표현될 수 있으며 Boolean Algebra 법칙, 규칙 및 정리가 적용될 수 있습니다. 부울 표현식은 디지털 논리 게이트의 이해를 용이하게 하는 스위칭 이론으로 표현할 수 있습니다.
디지털 로직 게이트에 대한 이해는 복잡한 로직 회로나 마이크로프로세서를 다룰 때 필수적입니다. 디지털 논리 게이트는 조합 및 순차 논리 회로의 기본 빌딩 블록입니다. 조합 논리 회로는 외부 입력 또는 적용된 신호에만 의존합니다. 반면, 순차 논리 회로는 현재 상태, 출력 및 외부에서 적용된 입력에 따라 달라집니다.
스위치 이론
스위치는 어느 방향으로든 전류의 흐름을 허용하기 위해 계전기의 전기 기계 접점이 될 수 있습니다.
Normal Open Switch
다음 회로에서는 전압원이 Normal Open 스위치를 통해 램프에 연결됩니다. 정상적인 조건 즉 스위치가 열린 상태에서는 전압원과 램프 사이의 전기 경로가 형성되지 않고 전류가 흐르지 않습니다. 램프가 켜지거나 켜지지 않습니다. 그러나 스위치가 닫힌 상태에서 전압원과 램프 사이의 전기 경로가 형성됩니다. 전압원에서 스위치를 통해 램프로 전류가 흘러 램프가 켜집니다.

그림 1: Normal Open 스위치
스위치 위치, 즉 "OFF/OPEN" 및 "ON/CLOSED"는 각각 "0" 및 "1"의 부울 상태와 동일합니다. 마찬가지로, 램프 상태는 각각 "0"과 "1"에 의해 "OFF" 및 "ON"입니다. 스위치는 입력(A)으로 표시되고 램프는 출력(L)으로 나타낼 수 있습니다.
스위치/입력(A)이 "0"으로 열리면 램프/출력(L)도 "0"으로 켜지거나 켜지지 않습니다. 마찬가지로 스위치/입력(A)이 "1"로 닫히면 램프/출력이 "1"로 켜지거나 켜집니다. 이는 아래에 표시된 등가 스위칭 진리표를 통해 설명할 수 있습니다.

위의 표에서 스위치는 램프, 즉 A = L과 같으며, 이는 스위치가 "OFF"일 때 램프도 "OFF"가 되고 이 현상은 스위치의 "ON" 상태에서 유지됨을 의미합니다. 위의 회로에 사용된 스위치는 상시 개방되어 있으며 물리적으로 접점을 만들어야 폐쇄된 것으로 간주됩니다. 다른 유형의 스위치는 상시 열림과 반대되는 상시 닫혀 있으며 열린 것으로 간주되기 위해 접점을 물리적으로 끊어야 합니다.
Normal Close 스위치
다음 회로에서 전압 소스는 Normal Close 스위치를 통해 램프에 연결됩니다. 정상적인 조건, 즉 스위치가 닫히면 전압 소스와 램프 사이의 전기 경로가 설정되고 전류가 흐르면서 램프를 비춥니다. 그러나 스위치를 누르면, 즉 스위치가 열리면 전압 소스와 램프 사이의 전기 경로가 끊어집니다. 램프의 조명과 함께 전류 흐름이 멈춥니다.

그림 2: Normal Close 스위치
여기서 스위치 위치, 즉 "OFF/OPEN" 및 "ON/CLOSED"는 각각 "1" 및 "0"의 부울 상태와 동일합니다.
위 전기 회로는 스위치/입력(A)이 "1" 열리면 램프/출력(L)이 "0"(켜지지 않음)이 되는 것으로 설명할 수 있습니다. 마찬가지로 스위치/입력(A)이 "0" 닫히면 램프/출력이 "1"(켜짐)이 됩니다. 이는 아래에 표시된 등가 스위칭 진리표를 통해 설명할 수 있습니다.
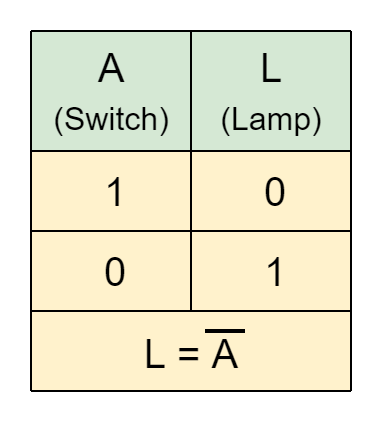
위의 표에서 스위치와 램프 상태는 서로 반대이므로 스위치가 "OFF"일 때 램프는 "ON"이 되고 마찬가지로 스위치가 "ON"이면 램프는 "OFF"가 됩니다. 상시 폐쇄 스위치는 스위칭 이론 측면에서 반전 기능을 수행합니다.
직렬 스위치 케이스
위의 회로에서 단일 스위치는 램프 작동을 제어하는 데 사용됩니다. 단일 스위치는 램프를 비추기 위해 램프에 전류의 흐름을 허용했습니다. 단일 스위치의 상태는 램프 상태와 동일합니다. 즉, 둘 다 동시에 "OFF" 또는 "ON"입니다. 첫 번째 스위치와 직렬로 스위치를 추가하면 다른 상황이 발생합니다.
전압원, 램프 및 두 개의 직렬 스위치를 가진 다음 회로를 생각해 보십시오. 스위치를 입력 "A"와 "B"로 표시할 수 있습니다. 열림/오프 상태는 "0"으로 표시되고 닫힘/온 상태는 "1"로 표시됩니다.
두 스위치는 램프를 제어하기 위해 총 네 가지 조합을 만듭니다. 첫 번째 조합은 A=0 & B=0, 두 번째 조합은 A=0 & B=1, 세 번째 조합은 A=1 & B=0, 네 번째 조합은 A=1 & B=1입니다. 램프에는 A와 B의 각 조합에 해당하는 네 가지 상태가 있습니다. 직렬의 물리적 스위치에서 알 수 있듯이 두 스위치가 닫히거나 논리적 "1" 상태일 때 전류가 전압원에서 램프로 흐릅니다.
직렬 스위치의 진리표는 다음과 같습니다:

그림 3: 직렬 스위치 구성
다음 진리표에서 보면, 두 스위치/입력이 모두 닫히거나 "1" 논리 상태에 있을 때 램프가 켜짐이 분명합니다("1"의 상태). 두 스위치 중 하나가 "0" 논리 상태에 있을 때 램프는 "0" 상태입니다. 이것은 L = A와 B 식으로 이어집니다. 부울 대수학에서, 이것은 논리곱 연산으로 입력 변수들, 즉 L=A.B 사이의 한 점(.) 점으로 표시됩니다.

따라서 스위칭 이론 및 직렬 스위치의 작동은 디지털 로직 "AND"게이트와 동일합니다.
디지털 로직 및 게이트
스위칭 이론 등가 논리 AND 게이트는 진리표와 함께 아래에 나와 있습니다. 스위치 "A"와 "B"는 함께 AND되어 출력 "Q"를 생성합니다.

그림 4: 스위칭 AND 게이트 및 진리표
병렬 스위치 케이스
전압원, 램프, 두 개의 병렬 스위치를 가진 다음 회로를 생각해 보자. 직렬 스위치와 유사하게 두 개의 병렬 스위치는 램프를 제어하기 위해 총 네 가지 조합을 만듭니다. 램프에는 A와 B의 각 조합에 해당하는 네 가지 상태가 있으며 현재 서로 병렬로 연결되어 있습니다. 병렬 스위치에서 알 수 있듯이 어떤 스위치가 닫히거나 논리적 "1" 상태에 있을 때 전류가 전압원에서 램프로 흐릅니다.
병렬 스위치의 진리표는 아래에 나와 있습니다.

그림 5: 병렬 스위치 케이스
진리표를 따르자면, 두 스위치/입력이 모두 열리거나 "0"의 논리 상태에 있을 때 램프가 켜지지 않음이 분명합니다("0"의 상태). 두 스위치 중 하나가 닫히거나 "1"의 논리 상태에 있을 때 램프가 켜집니다. 이것은 L = A 또는 B 식으로 이어집니다. 부울 대수학에서, 이것은 입력 변수들, 즉 L = A+B 사이의 더하기 (+)로 표시되는 논리곱 연산입니다.

따라서 스위칭 이론에서 병렬 스위치의 작동은 디지털 로직 "OR" 게이트와 동일합니다.
디지털 로직 OR 게이트
스위칭 이론 등가 논리 OR 게이트는 진리표와 함께 아래에 나와 있습니다. 스위치 "A"와 "B"는 출력 "Q"를 생성하기 위해 함께 OR로 처리됩니다.

그림 6: 스위칭 OR 게이트 및 진리표
스위치의 항등식의 법칙
스위칭 이론은 두 개의 서로 다른 스위치 또는 변수, 즉 "A"와 "B"를 갖는 등가적인 논리 AND 및 OR 게이트에 대해 논의합니다. 이 두 변수는 "A"와 같은 단일 변수와 논리 AND의 연산에 의해 제어될 수 있으며, 단일 변수에 대한 OR은 항등식 법칙(Idempotent Law)으로 정의된다.
항등식의 법칙에 따르면, 변수 자체의 AND'ing 또는 OR'ing은 원래 변수를 생성합니다. 즉, "A"와 "A"를 함께 사용하면 "A"가 생성되고 마찬가지로 AND 연산도 "A"를 생성합니다. 이것은 아래 그림과 같이 스위칭 회로를 단순화할 수 있습니다.
AND 함수의 항등식 법칙
AND 게이트에 해당하는 스위칭 이론과 함께 동일한 직렬 스위치를 구성하는 전기 회로는 다음과 같습니다.

그림 7: Idempotent AND 스위치와 동등
OR 기능의 항등식 법칙
동일한 병렬 스위치로 구성된 전기 회로와 OR 게이트에 해당하는 스위칭 이론은 다음과 같습니다.

그림 8: Idempotent OR 동급 스위치
부울 함수의 스위칭 이론
스위칭 이론에 따르면 직렬 스위치의 조합은 변수 사이에 점(.)으로 표시되는 논리적 AND(곱셈) 연산을 제공합니다. 마찬가지로, 직렬 스위치의 병렬 조합은 변수 사이에 더하기(+)로 표시되는 논리적 OR(합계) 연산을 제공합니다. 이러한 스위칭 이론을 사용하여 전기 회로에서 부울 함수를 구성할 수 있으며 그 반대의 경우도 마찬가지입니다.
스위칭 이론 예제
다음 그림에서 Q = (A+B)의 부울 함수입니다. C는 램프(Q)를 비추는 스위치를 사용하여 구현됩니다. 마찬가지로, 부울 함수는 스위칭 이론을 사용하여 스위칭 회로에서 얻을 수도 있습니다.

그림 9: 스위칭 이론의 예

그림 10: 예제 스위칭 회로의 논리 등가
'데이터계측분석 > 전기전자 기술자료' 카테고리의 다른 글
| 멀티플렉서 (0) | 2023.09.14 |
|---|---|
| 7세그먼트 디스플레이 디코더 (0) | 2023.09.14 |
| 부호 있는 이진수 (0) | 2023.09.14 |
| 하모닉스 - 고조파 (0) | 2023.09.14 |
| AC회로의 평균 및 RMS 전압 (0) | 2023.09.13 |